摘要:本文主要从五个层面探讨如何完整地构建出一个网络学习空间下的智慧学习系统,不仅从总体上进行了架构设计,而且对数据存储、学习者建模、知识建模都进行了科学地系统分析与代码实现。在最后的推送算法分析上,对以上各模块进行了汇总,从而衍生出了Dijkstra、UserCF、ItemCF、CAS等算法,对各类算法进行实现,并使用Top-N进行性能评估,再次优化,从而实现出一种高性能、高适用性的推送算法。以该算法为核心构建出的自适应智慧学习系统,这是一个复杂的教育生态系统,具有智能灵活、平衡和谐、可持续发展等特性,也只有这样一个算法才可以称得上是一个真正的学习共同体。
关键词:智慧学习系统,推荐算法,学习者建模,知识网络
ABSTRACT:This paper mainly discusses how to construct a kind of intelligent learning system under the network learning space from five aspects. It not only constructs the design from the whole, but also carries on the scientific system to the data storage, the learner modeling and the knowledge analysis and code implementation. In the final push algorithm analysis, the above modules are summarized, which derived Dijkstra, UserCF, ItemCF, CAS and other algorithms, the implementation of various algorithms, and the use of Top-N performance evaluation, re-optimization, which to achieve a high-performance, high applicability of the push algorithm. The adaptive intelligence learning system, which is based on the algorithm, is a complex educational ecosystem with intelligent and flexible, balanced and harmonious and sustainable development. Only one such algorithm can be regarded as a real learning community.
KEY WORDS:intelligent learning system, recommendation algorithm, learner modeling, knowledge network
1. 前言
1.1 背景分析
本论文定题为《在线学习资源智慧推送系统研究》,旨在设计出一款自适应的智慧学习系统,并着重于其推送算法的研究,使该智慧学习系统能够“智慧”地为学习者推送学习资源,打破以往学习者盲目地、零散地寻找教育信息的模式,让教育信息主动地去寻找对应的学习者,具有一定的主动性、个性化、智能化、高效性[1]。
本研究涉及教育领域、计算机领域、数学统计分析领域,具有一定的跨学科领域的特征。在教育上,本次研究的主体是学生,客体是教育信息资源(知识网络);在数学统计上,关键点是主客体建模,难点是研究出客体主动选择主体的推荐算法;在计算机软件上,基本点是构建系统,实现算法,并加以测试与应用。
本次研究的关键技术点在各自的领域都有所实现与应用,而作为核心的智慧推送,唯独在于教育领域没有过应用。原因在于“知识建模”的研究尚在起步阶段,国内外没有统一化标准[35];学习者建模又百家争鸣,没有定论。在单纯的推荐系统研究领域中,文献[10]中项亮博士就总结了一系列很好的推荐算法。在各大互联网平台中,例如国外的亚马孙、国内的美团,都设计了属于自己的一套性能高效、效果优良的推荐系统。在机器学习与统计学中,就有一系列的聚类分析与关联分析的算法,可是在智慧学习系统中没有学者提出过来使用。这其实是跨学科的缺点与教育领域的遗憾。本次研究即重点对“知识建模”进行探究与思考,对“学习者建模”的方法进行改进和完善,对已有的推荐算法进行整合与优化,从而在教育领域实现一套智慧推送系统。
本文主要从五个层面探讨如何完整地构建出一个网络学习空间下的智慧学习系统(图1),不仅从总体上进行了架构设计,而且对数据存储、学习者建模、知识建模都进行了科学地系统分析与代码实现。在最后的推送算法分析上,对以上各模块进行了汇总,从而衍生出了Dijkstra、UserCF、ItemCF、CAS等算法,对各类算法进行实现,并使用Top-N进行性能评估,再次优化,从而实现出一种高性能、高适用性的推送算法。以该算法为核心构建出的自适应智慧学习系统,这是一个复杂的教育生态系统,具有智能灵活、平衡和谐、可持续发展等特性[8],也只有这样一个算法才可以称得上是一个真正的学习共同体。
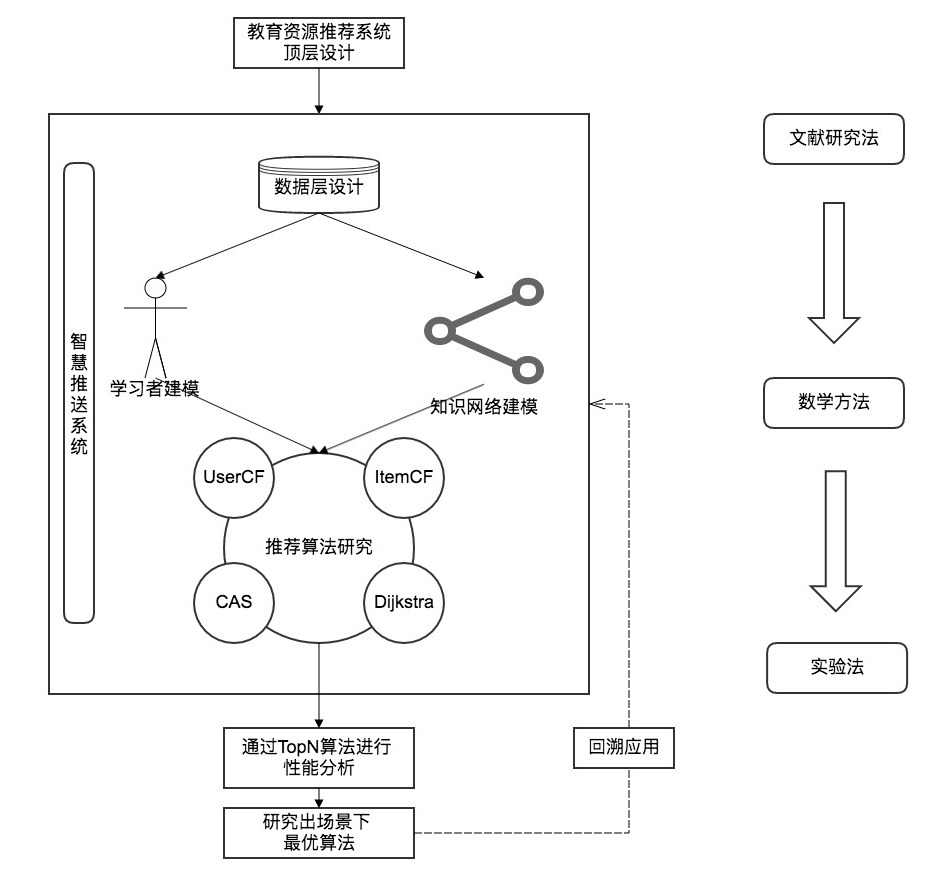
1.2 国内外现状
随着互联网技术的高速发展,一个又一个崭新的技术目不暇接地涌现出来,智慧学习就是其中之一。信息化极大地改变了人们的学习方式,以学生为中心、因材施教,当今学习活动日益变得个体化,学习依赖的环境更加数字化,学习场景泛在化,学习所依赖的环境、资源的属性越来越类似于消费类产品。[6]
对于智慧学习,在MBAlib中给出的定义是,智慧学习是学习者在智慧环境中按需获取学习资源,灵活自如开展学习活动,快速构建知识网络和人际网络的学习过程。智慧学习以发展学习者的学习智慧,提高学习者的创新能力为最终目标。作为在智慧教育理念指导下,在已有数字化学习、移动学习、泛在学习等基础上发展起来的一种新型学习方式。(MBAlib)
在2013的文献[16]中,韩国学者Hwang认为智慧学生是通过利用开放教育资源、 智能信息技术(Smart IT)和国际标准,使学习者的能力(基于行为改变)得以增强的一种较为灵活的学习[16]。在同年的文献[4]中,作者也曾深入的探讨过智慧学习的演进方向,“智慧学习”使人们将更多精力聚集于学习主题,默会地借助各种智能终端设备,无缝接入移动的泛在学习空间,灵活定制和透明访问最适宜、最便捷的资源服务,实现自我导向的主动学习[4]。
在文献[1]和文献[3]中,作者提出了推送服务的特点。在文献[2]中,作者对比了普通数字学习环境与智慧学习环境的差异,并提出了学习者建模技术这一概念。在文献[8]中,作者提出了智慧教育环境的系统模型设计,但是并没有设计出一个合理的系统。在文献[9]中,作者针对学习活动流,设计了一套较为完整的学习分析模型。综上可见,国内各学者对智慧学习的研究仍然仅仅停留在概念层面,即便有过模型研究,也只是针对推荐系统某一环节的建模研究,没有涉及到算法与可行性分析,是不完整的。
在去年(2016)年的文献[5]中,作者研究了智慧学习空间中学习行为分析及推荐系统的特点,该文中首先分析了网络学习空间中的行为特点,然后提出了学习推荐机制,对学习者进行了建模分析,之后在数据层也进行了比较完整的设计,并且最后提出了用户协同过滤算法与蚁群算法在推荐系统中的应用。该文设计了一套较为完整的智慧学习系统,但是对算法的研究没有到位,只是详细的分析了蚁群算法,缺少对性能的评估,没有对用户协同过滤算法进行研究、分析与实现,同时缺少对系统整体模型的把握,没有对知识网络进行建模。即便涉及到了数据层,但是缺少实现的技术。
以上智慧学习系统,对算法的缺失,对技术的缺失,可能只是在教育领域中才出现。在单纯的推荐系统研究领域中,文献[10]中项亮博士就总结了一系列很好的推荐算法。在各大互联网平台中,例如国外的亚马孙、国内的美团,都设计了属于自己的一套性能高效、效果优良的推荐系统。在机器学习与统计学中,就有一系列的聚类分析与关联分析的算法,可是在智慧学习系统中没有学者提出过来使用。这其实是跨学科的缺点与教育领域的遗憾。
2. 智慧学习系统顶层设计
2.1 智慧学习系统概述
在上文中提到了国内外各学者对于智慧学习的定义,综合之后亦可为智慧学习系统下定义:智慧学习系统是一种无缝式、由知识资源客体主动寻找学习行为主体的系统。
教育数据具有广泛性,学习过程具有自适性,具有这种广泛性与自适性,智慧学习系统应以学习分析技术为基础、以推送技术为核心,通过在线学习平台提供的学习环境,对教育数据进行挖掘和分析,为学习者提供反馈以改善学习行为。具体可以通过在线学习平台的大数据挖据,确定需要采集与分析的行为数据,之后进行学习者行为建模、学习者经历建模、学习者知识建模,将挖据和清理后的数据应用于这些模式之中,借由系统的预警性与预测性,分析学习者的学习趋势,研发干预模块,对学习者学习的内容与学习行为进行自适应调整、对学习路径进行优化,以加强学习者的学习效率、深化学习者的知识结构。同时,最为关键的,通过改进优化后的推荐算法,可以实现针对个体的“学习资源智慧推送”,以真正实现智慧学习系统的价值。
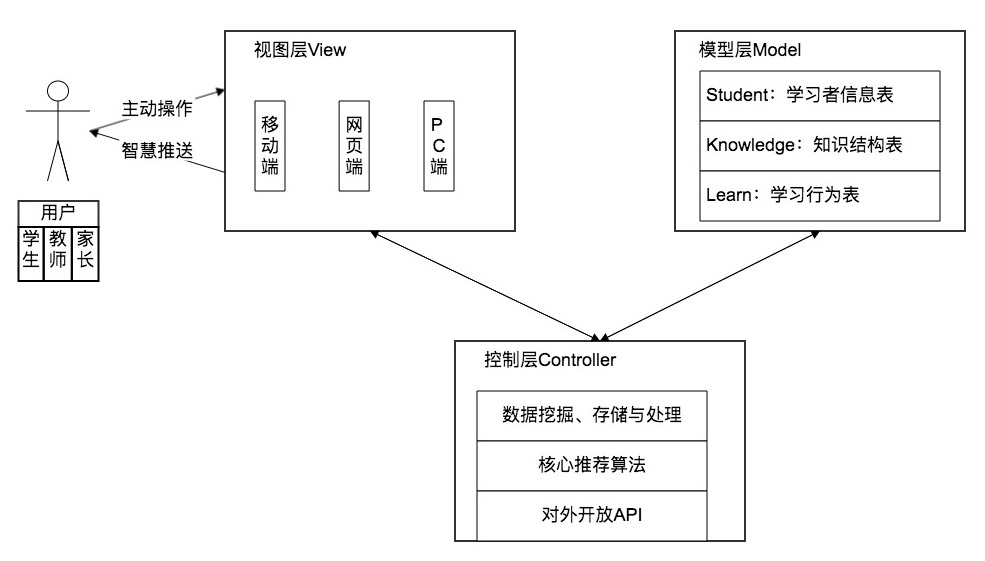
基于此,设计智慧学习系统架构如下图所示。整个系统基于MVC模式进行设计,视图层即在线学习平台,基于目前的网络空间,可包括移动端、网页端、PC端,其直接与用户进行交互。而该系统的用户也是多层次的,包括学生、家长、教师。模型层即系统数据库,用来存储系统产生的数据,主要存储的内容包括学习者基本信息、知识点信息、学习行为数据。控制层为整个系统的枢纽,提供数据分析与推荐算法,向视图层推送数据,向模型层转发数据。
2.2 智慧推送流程概述
智慧推送通过学习者的行为数据与知识点数据库中的数据进行匹配推荐,重点在于学习者特征建模,若数据信度不足以进行匹配建模,则需要扩大数据挖掘的范围与力度,直到数据足以支撑算法做到精准的推荐。推荐下一个知识点给学习者之后,学习者则根据推荐内容继续学习,数据挖掘系统则可进一步挖掘学习数据,给算法以更好的支撑。如此,这样一个闭合环路的推荐系统,可使推送的内容越来越精准,使用户的学习越来越高效,走在一个双赢共赢的良性循环的发展道路上。
st=>start: 起点
e=>end: 终点
op1=>operation: 使用系统进行学习
op2=>operation: 系统采集数据并分析
sub1=>subroutine: 扩大采集范围
cond=>condition: 是否满足算法
最低运算条件
op3=>operation: 推荐下一个知识点
st->op1->op2->cond
cond(yes)->op3->op1
cond(no)->sub1(right)->op22.3 数据层设计
2.3.1 数据层总体设计
智慧学习系统的基础是数据,没有数据就无从谈及算法,因此,该系统的数据层设计也尤为重要。
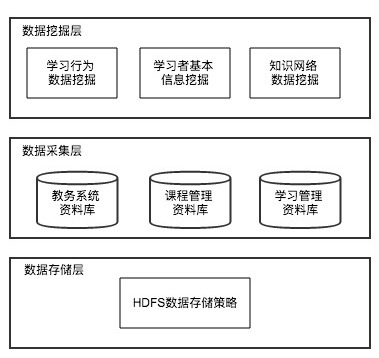
该系统将数据层更加细分为三个部分:数据挖掘层、数据采集层、数据存储层。数据挖掘层包括学习行为数据挖掘、学习者基本信息挖掘、知识网络数据挖掘;数据采集层的对象包括教务系统资料库、课程管理资料库、学习管理资料库;数据存储层则应用Hadoop提供HDFS数据存储层策略,对学习者特征信息、知识网络信息、学习行为信息进行大数据量的高效且安全的存储。
2.3.2 数据挖掘层与采集层的方案设计
郁晓华在文献[8]中设计了一套学习活动流,其在文中提供的学习行为抽取矩阵值得该系统的参考与借鉴。针对智慧学习系统的特征,对原矩阵进行一定的修改。学习者在系统中的学习行为主要有创建、标注、分享、选择、使用、保留等,获取各行为所调用的相关函数,并从教务系统资料库、课程管理资料库、学习管理资料库中,挖掘、采集到系统中的隐性数据,并进行存储。由此,新的学习行为抽取矩阵见下图,其本质也就是对动态信息数据的挖掘。

2.3.3 数据存储层设计
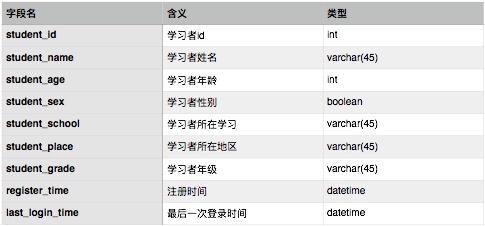
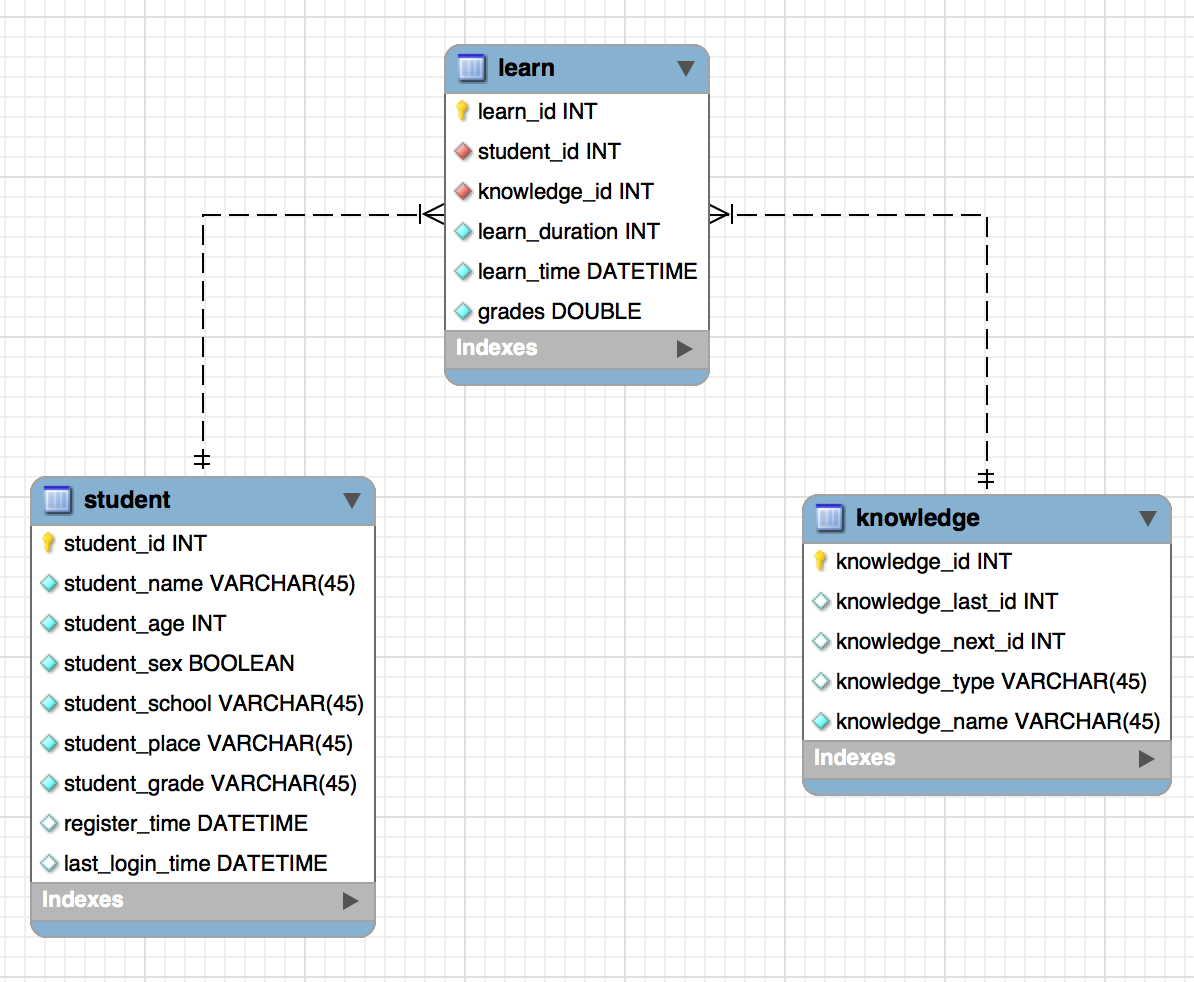
智慧学习系统的数据存储层应具有三大模块,以供存储三类数据:学习者数据、知识点数据、学习行为数据。基于此,可设计以下三张表供存储这三类数据,其中各表字段为系统基本信息,可根据实际情况进行扩展。
学习者信息表设计如下:
知识点信息表设计如下:
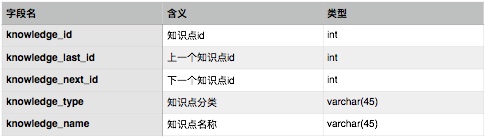
学习记录表设计如下:
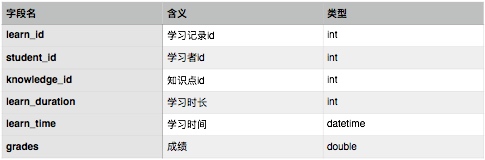
以上各表模型关系如下E-R图所示:
然而对于数据存储而言,其容灾机制是非常重要、必不可少的。这里采用HDFS的数据存储策略,将存储的数据拆成n个数据块,每个数据块各3个副本,分布在2个机架内的3个节点上,其中在机架1上有2份,另外一个机架上有1份。这样,即便是某个节点出现故障,也可以从本机架上的另外的节点上找到备份。例如,若下图中的DataNode1节点故障,那么数据块A可从本机架上的DataNode2节点获取备份,数据块C和D可从本机架上的DataNode3节点上获取备份。若故障严重,多个节点出现问题,甚至是整个机架发生故障,亦可从另一台机架上获取数据备份。
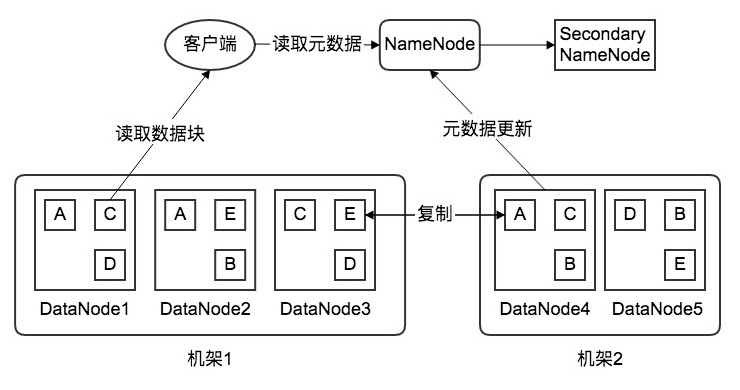
另外,各DataNode会不断地定时向NameNode发送心跳检测,报告自己的状态,包括网络状态、是否关机等信息。通过该心跳协议,NameNode可知道整个集群的运行状态。同时,二级NameNode会定期同步元数据映像文件和修改日志,当NameNode发送故障时,Secondary NameNode代替NameNode继续工作,以保证整个集群的正常运作,并且保障了整个系统的高可用性。
2.3.4 数据流处理方案
由上可见,智慧学习系统产生的数据量庞大,而推送系统又要具有高效性与实时性,因此,该系统对于数据流的处理能力也就提出了极高的要求。若不满足实现性、高效性,教育信息资源就无法做到精准且实时地推送给学习者,就会导致学习者学习行为效益出现滞后现象。智慧学习系统体现了教育信息化发展的新境界,它表达了一种技术以智慧性方式促进教育变革与创新的诉求,而这一目标的实现,必然离不开高效的学习分析技术[9]。其实,也就是对学习数据流的处理技术。
这里可考虑使用大数据处理的一种解决方案——MapReduce,是分治法的在数据处理中的一种应用。所谓分治,分而治之,即将一个大任务分成多个子任务,这个过程叫做Map;并行执行之后,合并结果,这个过程叫做Reduce。[31]
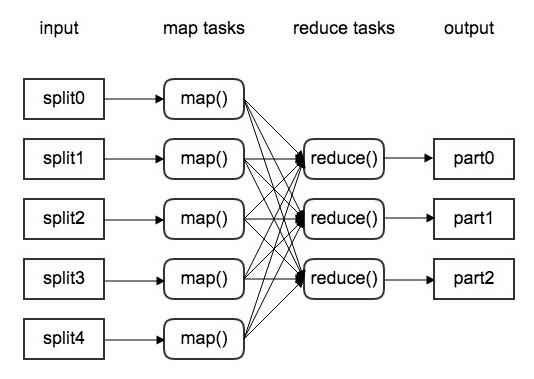
在Map阶段,首先是读数据,数据来源可能是文本文件、表格、数据库等,即智慧学习系统中时刻产生的行为数据。这些数据通常是成千上万的文件,叫做shards。这些shards被当做一个逻辑输入源,然后Map阶段调用用户实现的函数,叫做Mapper,独立且并行的处理每个shard。对于每个shard,Mapper返回多个键值对,这是Map阶段的输出。
在Map与Reduce之间的,叫做Shuffle阶段,即把键值对进行归类,也就是把所有相同的键的键值对归为一类。这个步骤的输出是不同的键和该键的对应的值的数据流。
在Reduce阶段,输入的是Shuffle的输出,然后Reduce阶段调用用户实现的函数,叫做Reducer,对每个不同的键和该键的对应的值的数据流进行独立、并行的处理。每个Reducer遍历键所对应的值,然后对值进行“置换”,这些置换通常指的是值的聚合,或是不处理,最后把键值对写入数据库中存储起来。
因此通过MapReduce,完成对大数据的高效处理,完全可应用于对数据流处理要求极高的智慧学习系统中。
3. 学习者特征分析与建模研究
3.1 学习者特征分析与建模概述
针对特定的推送问题,只是拥有数据还不够,想要从纷繁复杂的数据关系中挖掘出规律或模式,还得运用恰当的分析方法。比如聚类分析,恰当地选择运用聚类算法,可以按维度将数据适当的分群,根据各类的特征建立更有针对性的学习者模型,并实现更加精准的教育资源信息推送。
st=>start: 起点
e=>end: 终点
op1=>operation: 学习者聚类分析
op2=>operation: 学习者特征构建与选择
op3=>operation: 学习者建模与优化
st->op1->op2->op3->e特征对于精准推荐而言是相当重要的,在学习者建模之前的大部分工作都是在寻找特征,没有合适的特征的学习者模型,就几乎等于瞎猜,对智慧学习系统而言没有任何意义。特征通常是指输入数据中对因变量的影响比较明显的有趣变量或属性。特征分析方法主要有特征提取、特征构建与特征选择三种。特征提取,是指通过函数映射从原始特征中提取新特征的过程;而特征构建是从原始特征中推断或构建额外特征的过程;特征选择是指从原始的n个特征中选择m(m<n)个自特征的过程,从而按照某个标准实现了最优简化和降维(如下图所示)。对于智慧学习系统而言,原始数据本就是大量的、残缺的、隐性的,故不宜用特征提取,只适合特征构建与特征选择。
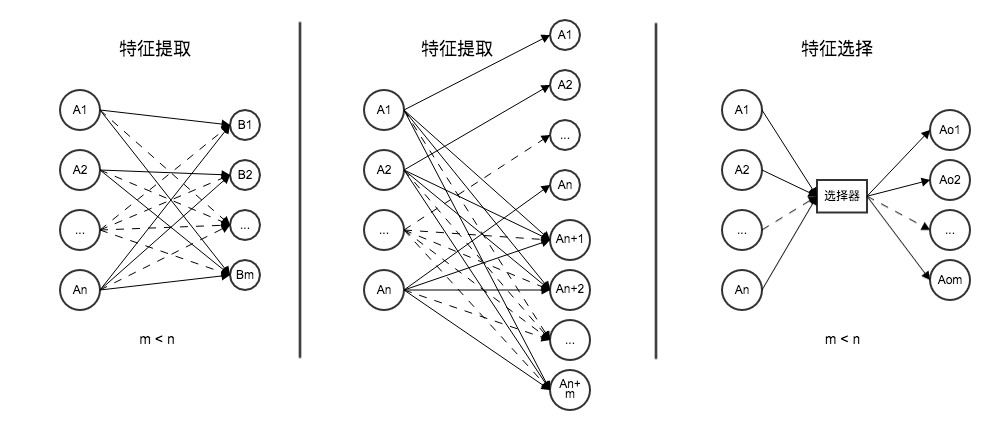
特征的构建与选取是建模之前的必要工作,甚至影响到了建模的成败,本节将就特征变换、特征组合方面简单谈谈学习者建模的基本步骤与方法,以期在不久的未来,供智慧学习系统的实现提供参考。
3.2 学习者聚类分析研究
聚类分析,简单来说,就是对学习者数据分群,它以学习者的相似性为基础,相同类中的样本比不同类中的样本更具相似性,以同来划分用户群,构建出不同层次、不同领域学习者群体。也只有将学习者进行聚类之后,才可能分别加以研究。因为学习者属性维度较多,该系统的聚类算法宜选用系统聚类算法,而非国内一些研究文献中提到的K-Means算法。
系统聚类算法首先将每个样本单独看成一类,在规定类间距离的条件下,选择距离最小的一堆合并成一个新类,并计算新类与其他类之间的距离,再将距离最近的两类合并,这样每次会减少一类,直到所有的样本合为一类为止。算法流程如下:
op1=>operation: 每样本单独成类
op2=>operation: 计算类间距离矩阵
op3=>operation: 合并距离最近的两类为新类
cond=>condition: 类的个数是否为1
op4=>operation: 画出聚类图
op5=>operation: 确定聚类数目和类别
op1->op2->op3->cond
cond(yes)->op4->op5
cond(no)->op2如下表所示,此处用6位学习者中的5个维度的学习行为数据作为样本,以欧式距离作为衡量样本间距离的标准,以最短距离法作为衡量类间距离的标准,以说明算法的流程与实践应用。

步骤1,将每个样本单独看成一类。
$G_1^{(0)}={x_1},G_2^{(0)}={x_2},G_3^{(0)}={x_3}$ $G_4^{(0)}={x_4},G_5^{(0)}={x_5},G_6^{(0)}={x_6}$
步骤2,计算各类之间的距离,得距离矩阵$D^{(0)}$。
$$ D^{(0)}= \begin{bmatrix} 0 & 9.540 & 8.660 & 4.900 & 4.690 & 6.780 \ 9.540 & 0 & 10.30 & 11.79 & 10.82 & 7.140 \ 8.660 & 10.30 & 0 & 11.09 & 9.330 & 10.15 \ 4.900 & 11.79 & 11.09 & 0 & 6.480 & 5.830 \ 4.690 & 10.82 & 9.330 & 6.480 & 0 & 8.120 \ 6.780 & 7.140 & 10.15 & 5.830 & 8.120 & 0 \ \end{bmatrix} $$
步骤3,矩阵$D^{(0)}$中的最小元素是4.690,它是$G_1^{(0)}$与$G_5^{(0)}$之间的距离,将它们合并,得到新类。 $G_1^{(1)}={x_1,x_5},G_2^{(1)}={x_2},G_3^{(1)}={x_3}$ $G_4^{(1)}={x_4},G_5^{(1)}={x_6}$
步骤4,计算各类之间的距离,得距离矩阵$D^{(1)}$,因$G_1^{(1)}$由$G_1^{(0)}$与$G_5^{(0)}$合并而成,按最短距离方法,分别计算$G_1^{(0)}$与$G_2^{(1)}$~$G_5^{(1)}$之间以及$G_5^{(0)}$与$G_2^{(1)}$~$G_5^{(1)}$之间的两两距离,并选其最小者作为两类间的距离。
$$ D^{(1)}= \begin{bmatrix} 0 & 9.540 & 8.660 & 4.900 & 6.780 \ 9.540 & 0 & 10.30 & 11.79 & 7.140 \ 8.660 & 10.30 & 0 & 11.09 & 10.15 \ 4.900 & 11.79 & 11.09 & 0 & 5.830 \ 6.780 & 7.140 & 10.15 & 5.830 & 0\ \end{bmatrix} $$
步骤5,矩阵$D^{(1)}$中的最小元素是4.900,它是$G_1^{(1)}$与$G_4^{(1)}$之间的距离,将它们合并,得到新类。
$G_1^{(2)}={x_1,x_4,x_5},G_2^{(2)}={x_2}$ $G_3^{(2)}={x_3},G_4^{(2)}={x_4}$
步骤6,计算各类之间的距离,得距离矩阵$D^{(2)}$。
$$ D^{(2)}= \begin{bmatrix} 0 & 9.540 & 8.660 & 5.830 \ 9.540 & 0 & 10.30 & 7.140 \ 8.660 & 10.30 & 0 & 10.15 \ 5.830 & 7.140 & 10.15 & 0 \ \end{bmatrix} $$
步骤7,矩阵$D^{(2)}$中的最小元素是5.830,它是$G_1^{(1)}$与$G_4^{(1)}$之间的距离,将它们合并,得到新类。
$G_1^{(3)}={x_1,x_4,x_5,x_6},G_2^{(3)}={x_2},G_3^{(3)}={x_3}$
步骤8,计算各类之间的距离,得距离矩阵$D^{(3)}$。
$$ D^{(3)}= \begin{bmatrix} 0 & 7.140 & 8.660 \ 7.140 & 0 & 10.30 \ 8.660 & 10.30 & 0 \ \end{bmatrix} $$
步骤9,矩阵$D^{(3)}$中的最小元素是7.140,它是$G_1^{(3)}$与$G_2^{(3)}$之间的距离,将它们合并,得到新类。
$G_1^{(4)}={x_1,x_2,x_4,x_5,x_6},G_2^{(4)}={x_3}$
步骤10,此时有两个类,最终可直接归为一类。
至此,便根据学习者的学习行为将学习者聚类完毕。
3.3 学习者特征构建技术与特征选择方法研究
3.3.1 特征构建
特征构建主要有特征变换与特征组合两种方法。特征变换指对原始的某个特征通过一定规则或映射得到新特征的方法。对于类别过大的分类变量,通常使用概念分层的方法变换得到类别较少的变量。比如有6位学习者的年级属性分别是初一、初二、高一、高二、大三、大四,那么通过概念分层之后,可将6位学习者分成3组,分别为初中、高中、大学。这种特征变换主要由人工的方式去完成,属于比较基础的特征构建方法。
特征组合指将两个或多个原始特征通过一定规则或映射得到新特征的方法。由于学习者特征多为非线性关系,所以数学分析的方法不好实用,宜实用基于特定领域知识的方法,以特定领域知识为基础,在一定的业务经验指导下实现。这种特征组合的方法也是主要由人工完成。如下图所示,便是一种学习者特征组合的方式之一,对比学习者的资料完善度、社区活跃度、作业完成率、考核得分率等信息,从而得出学习者积极性这一个区分度更加明确的特征。
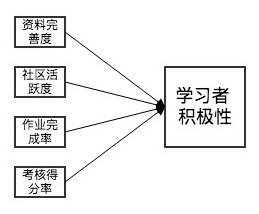
因此,在智慧学习系统构建学习者模型的这个阶段中,特征构建的方法宜用人工的方式去完成,须教育分析领域的专家对系统预试行阶段所采集的学习者数据进行研究与分析,结合其自身的领域知识,对学习者特征进行变换和组合,以构建区分度更强的特征。 ·
3.3.2 特征选择
在建立模型之前,我们已经按照特征构建的方法得到了数据集,然而这样的数据集其实还存在着大量的特征,特征之间可能存在相关性,还可能存在冗余的特征。为了提升建模效率,获取区分度更好的特征,需要对数据集进行降维处理,以得到最优子集,这个过程就是特征选择。
Gini 系数是衡量不平等性的指标,在分类问题中,分类数节点 A 的 Gini 系数表示样本在子集中被错分的可能性大小,它通常记作这个样本被选中的概率$p_i$乘以它被错分的概率$(1-p_i)$。例如响应变量 y 的取值有 k 个分类,令$p_i$是样本属于 i 类别的概率,则 Gini 系数的计算公式如下:
$Gini(A) = \sum_{i=1}^k p_i(1-p_i) = 1 - \sum_{i=1}^k p_i^2$
现举一例,以说明计算数据集中各特征 Gini 系数,并对特征进行排序的过程。如下表所示,系统采集到10个学生学习某门课程的数据,包括其是否完成过课程作业(X1)、学习该课程的频率(X2)、以及最后是否完成课程考核(Y)等情况,现通过对 Gini 系统的计算,判定特征 X1 与特征 X2 何者对结果 Y 更加重要。

步骤1,计算 X1 对 Y 的 Gini 系数。统计 X1 与 Y 的列联表如下表所示。

$Gini(X1 = 否) = 1 - ({2\over2+3})^2 - ({3\over2+3})^2 = 0.48$
$Gini(X1 = 是) = 1 - ({5\over5+0})^2 - ({5\over5+0})^2 = 0$
$Gini(X1) = {2+3\over2+3+5+0} · Gini(X1 = 否) + {5+0\over2+3+5+0} · Gini(X1 = 是) = 0.24$
步骤2,计算 X2 对 Y 的 Gini 系数。统计 X2 与 Y 的列联表如下表所示。
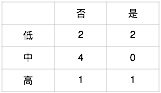
$Gini(X2 = 低) = 1 - ({2\over2+2})^2 - ({2\over2+2})^2 = 0.5$
$Gini(X2 = 中) = 1 - ({4\over4+0})^2 - ({0\over4+0})^2 = 0$
$Gini(X2 = 高) = 1 - ({1\over1+1})^2 - ({1\over1+1})^2 = 0.5$
$Gini(X2) = {4\over10} · Gini(X2 = 低) + {4\over10} · Gini(X2 = 中) + {2\over10} · Gini(X2 = 高) = 0.3$
步骤3,通过计算 X1 、 X2 的 Gini 系数,且有大小关系 Gini(X2) > Gini(X1),所以重要性顺序为: X1 > X2。
也就是在上例中,对于该生该门是否考核成功,是否完成作业会比学习课程的频率更加重要。同理,可通过对系统挖掘到各特征进行 Gini 系数的计算,过滤掉一些冗余特征,筛选出更好的特征,以供建模。
3.4 学习者用户画像及其建模研究
通过以上的特征构建与特征选择,即可勾画出学习者的用户画像。针对智慧学习系统而言,构建用户画像技术难点主要有以下6点:用户画像算法模型不断优化;引入 Storm 等实时技术;主题推荐标签、用户命名实体等新增标签补充进画像;HBase 的离线和在线分离、HBase 的 KV 读和 Solr 的批量读分离、region 热点监控和切分;数据流不断优化;数据存储改进。[26]
难题的根本起因是数据量的庞大、运算量的复杂、时效性的高要求,解决以上难题比较简单的一种方法就是实现 HBase 的离线和在线分离,采用离线和在线的两种方式,把可用性提上去。以下为一种解决方案的模型:
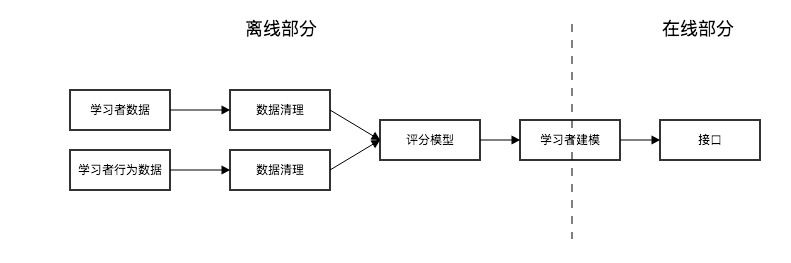
整个系统由数据驱动,通过研究数据,不断产生新的用户画像,优化学习者模型。而优化学习者模型,最为关键的是对模型的参加进行优化,以得到更优的模型。 ·
3.5 模型参数优化方案研究
对于学习者模型的参数优化,可选用的优化方法主要包括交叉验证、遗传算法、粒子群优化、模拟退火等。网络搜索计算成本太高,不宜采用。本节将就交叉验证、遗传算法、粒子群优化这三种算法,在智慧学习系统中做学习者模型优化的方式做简单探究。
3.5.1 使用交叉验证优化学习者模型
交叉验证的思想是将学习者数据集分割成 N 份,依次使用其中1份作为测试集,其他 N-1 份整合到一起作为训练集,将训练好的模型用于测试集上,以得到学习者模型好坏的判断或估计值,总计可以得到 N 个这样的值。交叉验证通常用于估计模型的误差,这里将 N 个对应的误差求平均作为对学习者模型的估计。同时,也可根据这 N 个值,选出拟合效果最好的学习者模型,对应学习者模型的参数也被认为是最优或接近最优的。
3.5.2 使用遗传算法优化学习者模型
遗传算法是模拟自然界遗传选择与淘汰的生物进化计算模型,根据自然选择选择学说的两个核心关键点——遗传和变异,来模拟生物进化机制,最终发展成为一种随机全局搜索和优化的算法。它的研究对象是种群,就是个体的集合,在该系统中即为某类学习者的集合,对应于求解的问题,这里的一个个体代表一个解,种群代表这些解的集合。在生物进化的过程开始阶段,所有的生物个体也许都不是最优的,同理,在模型求解的过程中,所有的解或许不是最优的,经过将这些解进行编码、选择、交叉、编译之后,逐代进化,从子代中可以找到求解问题的全局最优解。具体流程如下图所示。
op1=>operation: 产生初始种群
op2=>operation: 计算适应度
cond=>condition: 是否满足
优化准则
op3=>operation: 选择
op4=>operation: 交叉
op5=>operation: 变异
op6=>operation: 最佳个体
op1->op2->cond
cond(yes)->op6
cond(no)->op3(right)->op4(right)->op5(right)->op2通过遗传算法,可对学习者模型的一些参数进行优化,从而完善模型,产生最适应的学习者模型。
3.5.3 使用粒子群优化算法优化学习者模型
粒子群优化算法是通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。与遗传算法一样,它也是基于“种群”与“进化” 的概念,通过个体间的协作也竞争,从而实现复制空间最优解的搜索。但粒子群优化无需对个体进行选择、交叉、变异等进化操作,而是将种群中的个体看成是 D 维搜索空间中没有质量没有体积的粒子,每个粒子以一定的速度在解空间运动,并向例子本身历史最佳位置和种群历史最佳位置靠拢,从而实现对候选解的优化。算法流程如下图所示。
op1=>operation: 产生初始粒子群
op2=>operation: 计算每个粒子适应度
op3=>operation: 更新pbest、gbest
更新位置与速度
cond=>condition: 是否达到最大迭代次数,
最佳适应度增量小于阈值
op4=>operation: 算法终止
op1->op2->op3->cond
cond(yes)->op4
cond(no)->op2综上,可在智慧学习系统中,综合选择以上三种算法,对学习者模型的参数进行优化。
4. 知识网络建模研究
4.1 知识网络建模概述
学习者是智慧学习系统的对象,而知识网络则是学习系统的主要内容,所以对知识图谱的构建至关重要。不同于学习者模型,知识网络模型的静态数据来源居多,因而知识图谱的构建关键在于模型的合理选择。知识图谱属于复杂系统与复杂网络,其结构亦属于随机图论的一部分,同领域知识之间的规则性与跨领域知识之间的随机性在结构之中甚是突出。本节主要选取规则性和随机性并重的一些复杂网络模型—— WS 小世界网络模型、BA 无标度网模型与自组织耦合演化模型,探讨其与知识网络的契合性。
4.2 知识网络模型探究
4.2.1 WS 小世界网模型
通过简单的分析可以知道,知识网络结构兼具规则性与随机性。知识点在同领域内具有很强的规则性,前后衔接连贯,承前启后如一;而知识点在不同领域之间则具有很强的随机性,可能生物学的知识和天文学毫无关联,但和心理学、教育学、甚至是数学、统计学又有某些悬而未决的联系。小世界网络模型便是一种比较简单的、兼具规则性与随机性的一种复杂网络模型,下图便是 Watts & Strogatz 在《自然》杂志论文中显示的“小世界”随机图式[33]。
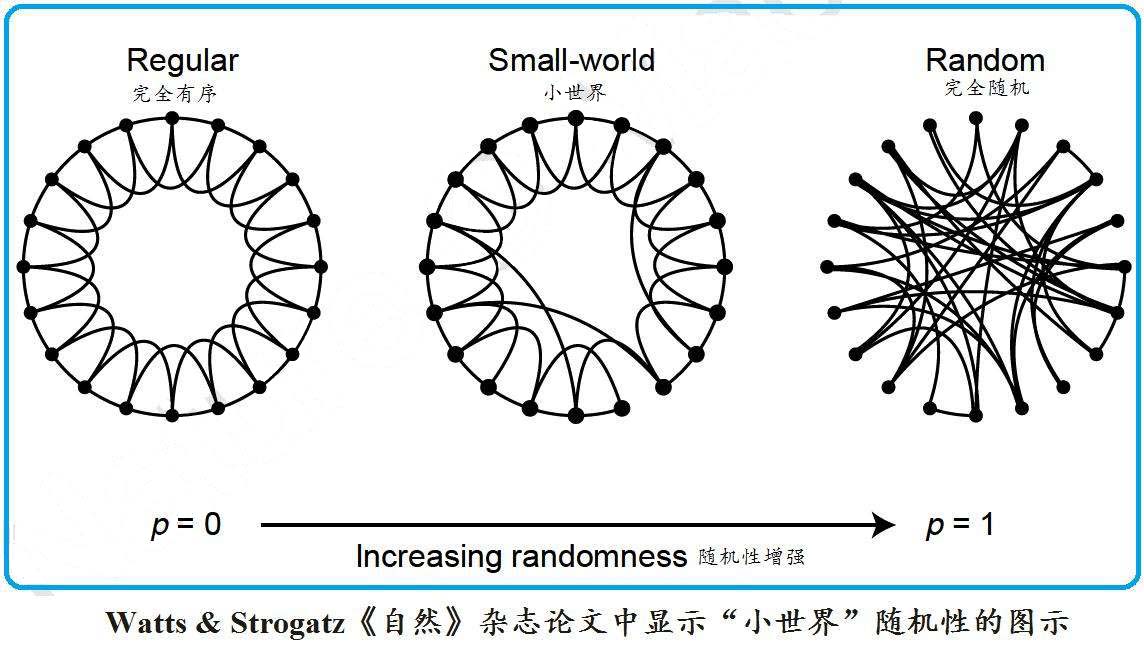
可见当 p = 0 时,没有随机跳跃边,是一个规则网模型;当 p = 1 时,所有边随机重连,是一个 ER 随机网模型。我们知道,同领域內知识规则性极大,且到达某一知识点不止唯一知识路径可走,会存在某些跳跃式的进程,单看这一点,其实小世界网模型还是比较契合同领域知识网络模型。
4.2.2 BA 无标度网模型
小世界网模型的“复杂”是一种“居于规则性与随机性之间”的简单的复杂,但仔细想想,知识网络不应该如此简单,也不应该如此静态。既然规则性与随机性都是简单的,那么复杂就不应该“简单地”位于它们之间。对于智慧学习系统所拥有的知识网络模型,我们不单单希望它有固定的结构,更希望它能够随着学习者知识量的增长而自我进化。
在初中刚学习菱形的面积计算时,我们会按照自己已有的知识结构通过面积等于底乘高的一半,即$S = {1\over2} ah$的公式去计算,而后我们发现其实对角线乘积的一半其实也等于面积,再纳入这一个特殊的情况下的公式之后,我们发现它其实可以推导至一般情况下使用,即对角线互相垂直的四边形的面积等于对角线乘积的一半。这样,我们就将四边形的面积公式纳入了自己的知识结构之中,在学习与应用之中,进化了自己的知识网络。
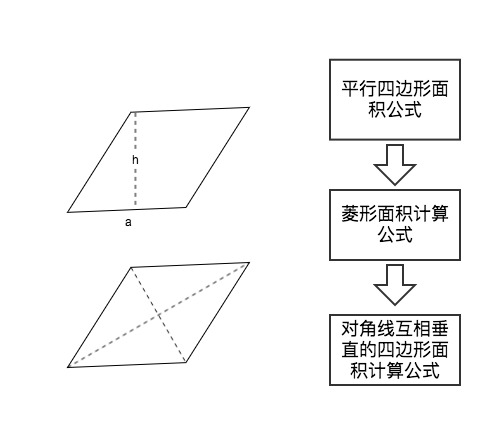
无标度网模型包含增长和优选这两个重要的要素。增长强调该网络是一个开放的系统,会有新的基本单元不断加入,节点总数不断增加;优选则强调节点链接新边的概率应该依赖其拥有的度[34]。在这两个要素上提出的知识网络模型表述如下:
首先,在 t = 0 时,具有较少的 $m_0$ 个节点,以后每个时间周期读取学习行为数据库,根据数据库的学习记录增加新的知识节点,接到 $m(m\le m_0)$个旧节点上。
其次,新节点连接到旧节点 i 的概率正比于其的度,这个度又正比于其置信度,所以连接概率为:$\prod(k_i) = k_i / \sum_{j=1}^{N-1}k_j$,其中 $k_i$ 表示旧知识节点 i 的置信度,N 表示知识网络节点数。
最后,根据以上步骤如此演化,直到达到一个稳定演化的状态,形成一套稳定的知识网络模型。
4.2.3 自组织耦合演化模型
然而知识网络模型宏大,更新模型需要周期性的扫描整个网络,这对智慧系统的计算量而言是一个极大的负担,因此需要建立基于局部相互作用机制的模型来了解能否从自组织动力学,来推导出整个知识网络的结构和特性。而自组织耦合演化模型,就是这样一个模型。
自组织耦合演化模型也称自适应网络模型,其根据生态分离现象与竞争排斥原理构建而成,能够根据局部信息引起连边关系的变化,从而导致宏观性质涌现网络模型,具有极强的可塑性。若能使用自组织耦合演化模型去拟合知识网络模型,则能优化智慧学习系统的性能,提高服务器运算效率。但就目前而言,对该模型国内外研究均处于一个初步的阶段,但愿在不久的未来,该理论能够更加成熟,以便应用于智慧学习系统的实践中。
4.3 知识网络关联分析研究
关联分析,可以从学习行为的历史数据中挖掘出知识点之间的内在规律,从而对各零散的知识点进行关联,使智慧学习系统有指导性地对学习者进行学习路径的推荐。
针对系统内知识点间的关系分析,宜使用比较成熟的 Apriori 算法。Apriori 算法包括两个主要步骤,首先迭代搜索出数据集中所有频繁项集,即支持度不小于设定阈值的项集;其次,利用频繁项集构造出满足最小置信度的关联规则。下图为该算法的具体流程图。
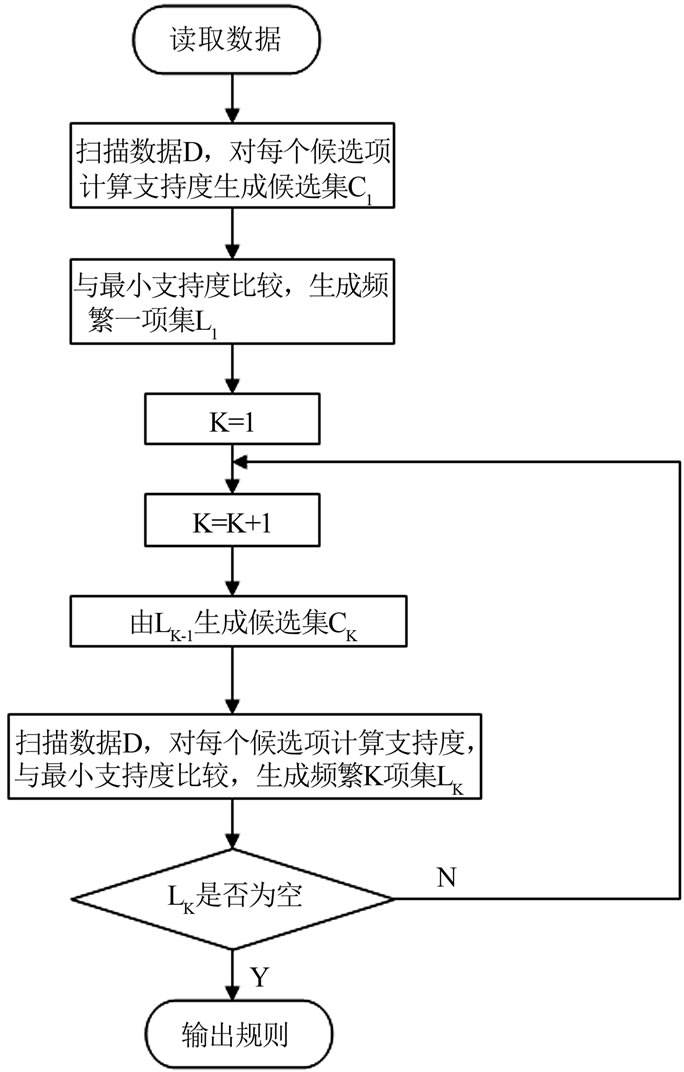
那么究竟如何使用 Apriori 算法去分析知识点间的关系,以形成知识网络呢?这里举一例以说明该算法在系统中的实践应用。例如这里有4位学习者的学习历史历史记录,1号学习者学过知识点A、C、D,2号学习者学过知识点B、C、E,3号学习者学习过知识点A、B、C、E,4号学习者学习过知识点B、E,列表如下。
| 学习者编号 | 知识点 |
|---|---|
| 1 | A,C,D |
| 2 | B,C,E |
| 3 | A,B,C,E |
| 4 | B,E |
首先,迭代搜索出以上四条数据的频繁项集。具体过程如下:
第1步,扫描数据集中的所有记录,生成候选1项集$C_1$,输出结果如下:
| 候选1项集 | 支持度计数 |
|---|---|
| {A} | 2 |
| {B} | 3 |
| {C} | 3 |
| {D} | 1 |
| {E} | 3 |
第2步,由上知最小支持度计数为2,所以剪去{D},生成频繁1项集$L_1$,输出结果如下:
| 频繁1项集 | 支持度计数 |
|---|---|
| {A} | 2 |
| {B} | 3 |
| {C} | 3 |
| {E} | 3 |
第3步,$L_1$自连接生成候选2项集$C_2$,因为此处$L_1$各集合只有一个项,两两结合即可,输出结果如下:
| 候选2项集 | 支持度计数 |
|---|---|
| {A,B} | 1 |
| {A,C} | 2 |
| {A,E} | 1 |
| {B,C} | 2 |
| {B,E} | 3 |
| {C,E} | 2 |
第4步,{A,B} 与 {A,E} 不满足最小支持度的要求,剪掉后生成频繁2项集$L_2$,输出结果如下:
| 频繁2项集 | 支持度计数 |
|---|---|
| {A,C} | 2 |
| {B,C} | 2 |
| {B,E} | 3 |
| {C,E} | 2 |
第5步,$L_2$自连接生成候选3项集$C_3$,此时$L_2$各集合中只有一个项不同其余项都相同的进行两两组合,输出结果如下:
| 候选3项集 | 支持度计数 |
|---|---|
| {A,B,C} | 1 |
| {A,C,E} | 1 |
| {B,C,E} | 2 |
第6步,{A,B,C} 和 {A,C,E} 不满足最小支持度的眼球,剪掉之后,发现 {A,B,C} 的 2 项子集 {A,B} 与 {A,C,E} 的 2 项子集 {A,E} 都不在 $L_2$ 中,因此也是不频繁的,应该去掉,生成频繁 3 项集 $L_3$,输出结果如下:
| 频繁3项集 | 支持度计数 |
|---|---|
| {B,C,E} | 2 |
因此,得到最终结果频繁项集$L_3 = {B,C,E}$ ,且它的任何 2 项子集都是频繁的。得到频繁项集之后,则需要构造出满足给定最小置信度的关联规则。如果满足$c(S \Rightarrow C_LS) \ge min_conf$,那么输出规则$S \Rightarrow C_LS$,其中$C_LS$表示 S 在 L 中的补集。对于 $L_3$,它的非空子集有 {B}、{C}、{E}、{B,C}、{B,E}、{C,E}。置信度计算公式如下:
$c(A \Rightarrow B) = {{\sigma(A \Rightarrow B)} \over || T \in D | A \subseteq T ||} = {{|| T \in D | A \cup B \subseteq T ||} \over ||T \in D | A \subseteq T||}$
其中 T 表示事务,D 表示所有事务,$\sigma(A \Rightarrow B)$ 代表支持度计数。
根据公式计算出各自的关联规则及置信度如下表:
| 关联规则 | 置信度 |
|---|---|
| $B \Rightarrow CE$ | 0.67 |
| $C \Rightarrow BE$ | 0.67 |
| $E \Rightarrow BC$ | 0.67 |
| $BC \Rightarrow E$ | 1.00 |
| $BE \Rightarrow C$ | 0.67 |
| $CE \Rightarrow B$ | 1.00 |
若这里假设 min_conf = 0.9,则$BC \Rightarrow E$ 与 $CE \Rightarrow B$为强关联规则,也就是学习了知识点 B、C 之后可以进行 E 的学习,或学习了知识点 C、E 之后可以进行 B 的学习。至此,就得出了知识点间的关联关系,这对构建知识网络模型不失为一种科学有效的数学分析方法。
5. 推送算法研究
5.1 推送算法概述
对于智慧学习系统而言,推送算法是系统的灵魂。对知识点的推荐是否准确,是否适合学习者,直接决定了学习者的学习方向与其学习成果。然而,之前智慧学习系统的顶层架构研究,其实也是推送算法的框架;学习者是算法的对象,知识网络是算法分析的内容,因此对学习者和知识网络的建模,其实也是推送算法的一部分。
本节将就Dijkstra算法、用户协同过滤算法、物品协同过滤算法、混沌蚁群算法做阐述与研究,编码推荐算法,使用 TopN 测试算法性能,并在最后优化改进算法,形成一套最契合智慧学习系统灵魂的推送算法。
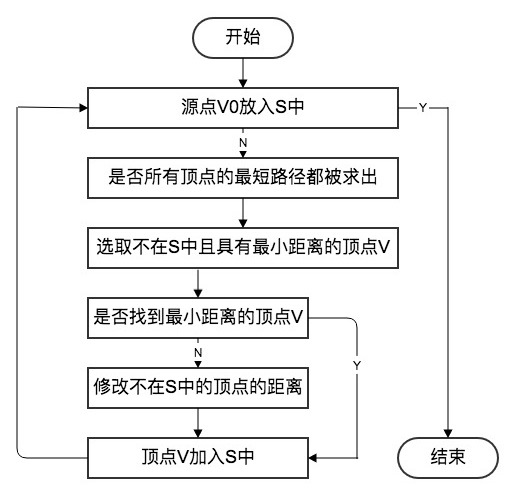
5.2 Dijkstra 算法
Dijkstra 算法是典型的单源最短路径算法,用于计算某个节点到其他所有节点的最短路径。Dijkstra 算法流程图如下。
在智慧学习系统对学习者建模与聚类分析之后,对某个学习者进行教育信息资源的推送,需要先对该学习者进行归类,之后根据该类学习者的学习行为历史记录,进行知识网络的关联分析,同时计算出该类学习者学习该知识网络内所有学习路径所耗费的平均时间,将知识点间耗费的平均学习时间作为度,构建出如下图谱。
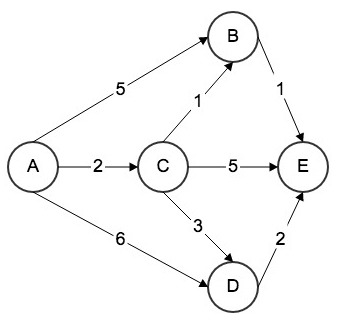
如上图所示,为某类学习者的知识网络的详细情况,图中的五个节点ABCDE代表知识点,节点之间的有向边代表学习路径,边上的度代表学习该路径所需要的单位平均时间。现有一位新加入该学习路径的学习者需要获取学习资源,那么智慧学习系统便可以使用 Dijsktra 单源最短路径算法进行资源的推荐。具体流程如下。
步骤1,计算知识点A到与之直接相连的知识点B、C、D的耗时,统计出表如下所示。
| 终点 | 路径 | 耗时 | 是否最短 |
|---|---|---|---|
| B | $A \rightarrow B$ | 5 | 未知 |
| C | $A \rightarrow C$ | 2 | 是 |
| D | $A \rightarrow D$ | 6 | 未知 |
| E | 未知 | 未知 | 未知 |
步骤2,根据上表,由松弛操作原理可知,$A \rightarrow C$ 为最短路径,耗时单位时间2。接着,计算知识点C到与之直接相连的知识点B、D、E的耗时,统计出表如下所示。
| 终点 | 路径 | 耗时 | 是否最短 |
|---|---|---|---|
| B | $A \rightarrow C \rightarrow B$ | 2 + 1 = 3 | 是 |
| C | $A \rightarrow C$ | 2 | 是 |
| D | $A \rightarrow C \rightarrow D$ | 2 + 3 = 6 | 未知 |
| E | $A \rightarrow C \rightarrow E$ | 2 + 5 = 7 | 未知 |
步骤3,根据上表,由松弛操作原理可知,$A \rightarrow C \rightarrow B$小于$A \rightarrow B$,为最短路径,耗时单位时间3。接着,计算知识点B到与之直接相连的知识点E的耗时,统计出表如下所示。
| 终点 | 路径 | 耗时 | 是否最短 |
|---|---|---|---|
| B | $A \rightarrow C \rightarrow B$ | 2 + 1 = 3 | 是 |
| C | $A \rightarrow C$ | 2 | 是 |
| D | $A \rightarrow C \rightarrow D$ | 2 + 3 = 5 | 未知 |
| E | $A \rightarrow C \rightarrow B \rightarrow E$ | 2 + 1 + 1 = 4 | 是 |
步骤4,根据上表,由松弛操作原理可知,$A \rightarrow C \rightarrow B \rightarrow E$小于$A \rightarrow C \rightarrow E$,为最短路径,耗时单位时间4。接着,计算知识点E到与之直接相连的知识点的耗时,由于知识点E无法到达其他节点,所以最终结果如表所示。
| 终点 | 路径 | 耗时 | 是否最短 |
|---|---|---|---|
| B | $A \rightarrow C \rightarrow B$ | 2 + 1 = 3 | 是 |
| C | $A \rightarrow C$ | 2 | 是 |
| D | $A \rightarrow C \rightarrow D$ | 2 + 3 = 5 | 是 |
| E | $A \rightarrow C \rightarrow B \rightarrow E$ | 2 + 1 + 1 = 4 | 是 |
综上,知识网络最短路径树如图所示。
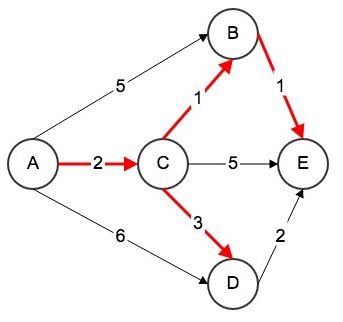
因此,智慧学习系统应推荐上图中的红色学习路径给这位学习者,这样学习者可花费最少的学习时间,用最高的学习效率学完这五个知识点。
以下为 C++ 语言的 Dijkstra 算法实现。
Dijkstra(Graph &graph, int s) : G(graph) {
this->s = s;
distTo = new Weight[G.V()];
marked = new bool[G.V()];
for (int i = 0; i < G.V(); i++) {
distTo[i] = Weight();
marked[i] = false;
from.push_back(NULL);
}
IndexMinHeap<Weight> ipq(G.V());
// start dijkstra
distTo[s] = Weight();
ipq.insert(s, distTo[s]);
marked[s] = true;
while (!ipq.isEmpty()) {
int v = ipq.extractMinIndex();
// distTo[v]就是s到v的最短距离
marked[v] = true;
typename Graph::adjIterator adj(G, v);
for (Edge<Weight> *e = adj.begin(); !adj.end(); e = adj.next()) {
int w = e->other(v);
if (!marked[w]) {
if (from[w] == NULL || distTo[v] + e->wt() < distTo[w]) {
distTo[w] = distTo[v] + e->wt();
from[w] = e;
if (ipq.contain(w))
ipq.change(w, distTo[w]);
else
ipq.insert(w, distTo[w]);
}
}
}
}
}接下来需要研究如何将此算法嵌入智慧学习系统之中。
首先先将上述知识网络转化成如下邻接表。
A B 5
A C 2
A D 6
B E 1
C B 1
C E 5
C D 3
D E 2为了方便程序读取,将A~E对应转换成0~4,并在首行添加上知识节点的个数与路径的边数,保存为 testG1.txt 如下所示。
5 8
0 1 5
0 2 2
0 3 6
1 4 1
2 1 1
2 4 5
2 3 3
3 4 2因为知识网络为有向图,所以先编写有向图处理程序 Edge.h,如下所示。
#include <iostream>
#include <cassert>
using namespace std;
template<typename Weight>
class Edge {
private:
int a, b;
Weight weight;
public:
Edge(int a, int b, Weight weight) {
this->a = a;
this->b = b;
this->weight = weight;
}
Edge() {}
~Edge() {}
int v() { return a; }
int w() { return b; }
Weight wt() { return weight; }
int other(int x) {
assert(x == a || x == b);
return x == a ? b : a;
}
friend ostream &operator<<(ostream &os, const Edge &e) {
os << e.a << "-" << e.b << ": " << e.weight;
return os;
}
bool operator<(Edge<Weight> &e) {
return weight < e.wt();
}
bool operator<=(Edge<Weight> &e) {
return weight <= e.wt();
}
bool operator>(Edge<Weight> &e) {
return weight > e.wt();
}
bool operator>=(Edge<Weight> &e) {
return weight >= e.wt();
}
bool operator==(Edge<Weight> &e) {
return weight == e.wt();
}
};接着对应不同的知识网络的疏密程度,分别编写稀疏图数据结构 SparseGraph.h 与稠密图数据结构 DenseGraph.h,如下所示。
#include <iostream>
#include <vector>
#include <cassert>
#include "Edge.h"
using namespace std;
// 稀疏图 - 邻接表
template<typename Weight>
class SparseGraph {
private:
int n, m;
bool directed;
vector<vector<Edge<Weight> *> > g;
public:
SparseGraph(int n, bool directed) {
this->n = n;
this->m = 0;
this->directed = directed;
for (int i = 0; i < n; i++)
g.push_back(vector<Edge<Weight> *>());
}
~SparseGraph() {
for (int i = 0; i < n; i++)
for (int j = 0; j < g[i].size(); j++)
delete g[i][j];
}
int V() { return n; }
int E() { return m; }
void addEdge(int v, int w, Weight weight) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
g[v].push_back(new Edge<Weight>(v, w, weight));
if (v != w && !directed)
g[w].push_back(new Edge<Weight>(w, v, weight));
m++;
}
bool hasEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
for (int i = 0; i < g[v].size(); i++)
if (g[v][i]->other(v) == w)
return true;
return false;
}
void show() {
for (int i = 0; i < n; i++) {
cout << "vertex " << i << ":\t";
for (int j = 0; j < g[i].size(); j++)
cout << "( to:" << g[i][j]->w() << ",wt:" << g[i][j]->wt() << ")\t";
cout << endl;
}
}
class adjIterator {
private:
SparseGraph &G;
int v;
int index;
public:
adjIterator(SparseGraph &graph, int v) : G(graph) {
this->v = v;
this->index = 0;
}
Edge<Weight> *begin() {
index = 0;
if (G.g[v].size())
return G.g[v][index];
return NULL;
}
Edge<Weight> *next() {
index += 1;
if (index < G.g[v].size())
return G.g[v][index];
return NULL;
}
bool end() {
return index >= G.g[v].size();
}
};
};#include <iostream>
#include <vector>
#include <cassert>
#include "Edge.h"
using namespace std;
// 稠密图 - 邻接矩阵
template<typename Weight>
class DenseGraph {
private:
int n, m;
bool directed;
vector<vector<Edge<Weight> *> > g;
public:
DenseGraph(int n, bool directed) {
this->n = n;
this->m = 0;
this->directed = directed;
for (int i = 0; i < n; i++) {
g.push_back(vector<Edge<Weight> *>(n, NULL));
}
}
~DenseGraph() {
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (g[i][j] != NULL)
delete g[i][j];
}
int V() { return n; }
int E() { return m; }
void addEdge(int v, int w, Weight weight) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
if (hasEdge(v, w)) {
delete g[v][w];
if (!directed)
delete g[w][v];
m--;
}
g[v][w] = new Edge<Weight>(v, w, weight);
if (!directed)
g[w][v] = new Edge<Weight>(w, v, weight);
m++;
}
bool hasEdge(int v, int w) {
assert(v >= 0 && v < n);
assert(w >= 0 && w < n);
return g[v][w] != NULL;
}
void show() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
if (g[i][j])
cout << g[i][j]->wt() << "\t";
else
cout << "NULL\t";
cout << endl;
}
}
class adjIterator {
private:
DenseGraph &G;
int v;
int index;
public:
adjIterator(DenseGraph &graph, int v) : G(graph) {
this->v = v;
this->index = -1;
}
Edge<Weight> *begin() {
index = -1;
return next();
}
Edge<Weight> *next() {
for (index += 1; index < G.V(); index++)
if (G.g[v][index])
return G.g[v][index];
return NULL;
}
bool end() {
return index >= G.V();
}
};
};另外,需要 ReadGraph.h 将图从文件中读进来:
#include <iostream>
#include <string>
#include <fstream>
#include <sstream>
#include <cassert>
using namespace std;
template<typename Graph, typename Weight>
class ReadGraph {
public:
ReadGraph(Graph &graph, const string &filename) {
ifstream file(filename);
string line;
int V, E;
assert(file.is_open());
assert(getline(file, line));
stringstream ss(line);
ss >> V >> E;
assert(graph.V() == V);
for (int i = 0; i < E; i++) {
assert(getline(file, line));
stringstream ss(line);
int a, b;
Weight w;
ss >> a >> b >> w;
assert(a >= 0 && a < V);
assert(b >= 0 && b < V);
graph.addEdge(a, b, w);
}
}
};接着需要最小索引堆 IndexMinHeap.h 进行算法优化,代码如下:
#include <iostream>
#include <algorithm>
#include <cassert>
using namespace std;
template<typename Item>
class IndexMinHeap {
private:
Item *data;
int *indexes;
int *reverse;
int count;
int capacity;
void shiftUp(int k) {
while (k > 1 && data[indexes[k / 2]] > data[indexes[k]]) {
swap(indexes[k / 2], indexes[k]);
reverse[indexes[k / 2]] = k / 2;
reverse[indexes[k]] = k;
k /= 2;
}
}
void shiftDown(int k) {
while (2 * k <= count) {
int j = 2 * k;
if (j + 1 <= count && data[indexes[j]] > data[indexes[j + 1]])
j += 1;
if (data[indexes[k]] <= data[indexes[j]])
break;
swap(indexes[k], indexes[j]);
reverse[indexes[k]] = k;
reverse[indexes[j]] = j;
k = j;
}
}
public:
IndexMinHeap(int capacity) {
data = new Item[capacity + 1];
indexes = new int[capacity + 1];
reverse = new int[capacity + 1];
for (int i = 0; i <= capacity; i++)
reverse[i] = 0;
count = 0;
this->capacity = capacity;
}
~IndexMinHeap() {
delete[] data;
delete[] indexes;
delete[] reverse;
}
int size() {
return count;
}
bool isEmpty() {
return count == 0;
}
void insert(int index, Item item) {
assert(count + 1 <= capacity);
assert(index + 1 >= 1 && index + 1 <= capacity);
index += 1;
data[index] = item;
indexes[count + 1] = index;
reverse[index] = count + 1;
count++;
shiftUp(count);
}
Item extractMin() {
assert(count > 0);
Item ret = data[indexes[1]];
swap(indexes[1], indexes[count]);
reverse[indexes[count]] = 0;
reverse[indexes[1]] = 1;
count--;
shiftDown(1);
return ret;
}
int extractMinIndex() {
assert(count > 0);
int ret = indexes[1] - 1;
swap(indexes[1], indexes[count]);
reverse[indexes[count]] = 0;
reverse[indexes[1]] = 1;
count--;
shiftDown(1);
return ret;
}
Item getMin() {
assert(count > 0);
return data[indexes[1]];
}
int getMinIndex() {
assert(count > 0);
return indexes[1] - 1;
}
bool contain(int index) {
return reverse[index + 1] != 0;
}
Item getItem(int index) {
assert(contain(index));
return data[index + 1];
}
void change(int index, Item newItem) {
assert(contain(index));
index += 1;
data[index] = newItem;
shiftUp(reverse[index]);
shiftDown(reverse[index]);
}
};紧接着,最为核心是编写 Dijkstra 算法的代码,Dijkstra.h 代码如下:
#include <iostream>
#include <vector>
#include <stack>
#include "Edge.h"
#include "IndexMinHeap.h"
using namespace std;
template<typename Graph, typename Weight>
class Dijkstra {
private:
Graph &G;
int s;
Weight *distTo;
bool *marked;
vector<Edge<Weight> *> from;
public:
Dijkstra(Graph &graph, int s) : G(graph) {
this->s = s;
distTo = new Weight[G.V()];
marked = new bool[G.V()];
for (int i = 0; i < G.V(); i++) {
distTo[i] = Weight();
marked[i] = false;
from.push_back(NULL);
}
IndexMinHeap<Weight> ipq(G.V());
// start dijkstra
distTo[s] = Weight();
ipq.insert(s, distTo[s]);
marked[s] = true;
while (!ipq.isEmpty()) {
int v = ipq.extractMinIndex();
// distTo[v]就是s到v的最短距离
marked[v] = true;
// cout<<v<<endl;
typename Graph::adjIterator adj(G, v);
for (Edge<Weight> *e = adj.begin(); !adj.end(); e = adj.next()) {
int w = e->other(v);
if (!marked[w]) {
if (from[w] == NULL || distTo[v] + e->wt() < distTo[w]) {
distTo[w] = distTo[v] + e->wt();
from[w] = e;
if (ipq.contain(w))
ipq.change(w, distTo[w]);
else
ipq.insert(w, distTo[w]);
}
}
}
}
}
~Dijkstra() {
delete[] distTo;
delete[] marked;
}
Weight shortestPathTo(int w) {
assert(w >= 0 && w < G.V());
return distTo[w];
}
bool hasPathTo(int w) {
assert(w >= 0 && w < G.V());
return marked[w];
}
void shortestPath(int w, vector<Edge<Weight> > &vec) {
assert(w >= 0 && w < G.V());
stack<Edge<Weight> *> s;
Edge<Weight> *e = from[w];
while (e->v() != this->s) {
s.push(e);
e = from[e->v()];
}
s.push(e);
while (!s.empty()) {
e = s.top();
vec.push_back(*e);
s.pop();
}
}
void showPath(int w) {
assert(w >= 0 && w < G.V());
vector<Edge<Weight> > vec;
shortestPath(w, vec);
for (int i = 0; i < vec.size(); i++) {
cout << vec[i].v() << " -> ";
if (i == vec.size() - 1)
cout << vec[i].w() << endl;
}
}
};最后编写主程序 main.cpp 运行代码,计算出最短学习路径。
#include <iostream>
#include "SparseGraph.h"
#include "DenseGraph.h"
#include "ReadGraph.h"
#include "Dijkstra.h"
using namespace std;
int main() {
string filename = "testG1.txt";
int V = 5;
SparseGraph<int> g = SparseGraph<int>(V, true);
//SparseGraph<int> g = SparseGraph<int>(V, false);
ReadGraph<SparseGraph<int>, int> readGraph(g, filename);
cout << "Test Dijkstra:" << endl << endl;
Dijkstra<SparseGraph<int>, int> dij(g, 0);
for (int i = 1; i < V; i++) {
cout << "Shortest Path to " << i << " : " << dij.shortestPathTo(i) << endl;
dij.showPath(i);
cout << "----------" << endl;
}
return 0;
}运行结果如下所示:
Test Dijkstra:
Shortest Path to 1 : 3
0 -> 2 -> 1
----------
Shortest Path to 2 : 2
0 -> 2
----------
Shortest Path to 3 : 5
0 -> 2 -> 3
----------
Shortest Path to 4 : 4
0 -> 2 -> 1 -> 4
----------可见,与手动算法分析所得结果完全一致。至此,将此段代码汇入系统,可向学习者推荐效率最高的学习路径。
5.3 协同过滤算法
协同过滤算法是诞生最早,也是一种较为著名的推荐算法,主要功能是进行预测与推荐。在智慧学习系统中使用协同过滤算法,主要是通过学习者的学习行为的历史数据去挖掘发现学习者的学习偏好,进而总结出该类学习者的学习规律。而这种仅仅基于学习者行为数据设计的推荐算法,就叫做协同过滤算法。而基于用户的协同过滤算法(User-based Collaborative filtering)、基于物品的协同过滤算法(Item-based Collaborative filtering),都属于基于领域的算法,同时也是协同过滤最为广泛实用的两种算法。
其中,基于用户的协同过滤算法会给学习者推荐和他学习路径相似的其他学习的优秀学习路径,基于物品的协同过滤算法会给学习者推荐它之前学习的知识点相似的学习路径。简而言之就是:人以类聚,物以群分。本节将分别说明这两类推荐算法的原理及其在智慧学习系统的实现方法。
5.3.1 基于用户的协同过滤算法
在智慧学习系统中应用基于用户的协同过滤算法,就是通过不同学习者对知识网络的学习行为来评测学习者之间的相似性,这一过程其实就是学习者的聚类,之后基于学习者的相似性进行推荐。简而言之就是:给学习者推荐与他学习行为相似的其他学习者的学习路径。下面举一例,以说明基于用户的协同过滤算法的流程。
现在有4名学习者,各自学习过的知识点如下表所示,现运用基于用户的协同过滤算法,给学习者A推荐下一个知识点的教育信息资源。
| 学习者 | 学习行为 |
|---|---|
| A | a,b,d |
| B | a,c |
| C | b,e |
| D | c,d,e |
第一步,采用余弦相似度计算学习者A与其他3位学习者之间的相似度:
$W_{AB} = {|{a,b,d} \cap {a,c}|\over \sqrt{|{a,b,d}| |{a,c}|}} = {1 \over \sqrt6} $
$W_{AC} = {|{a,b,d} \cap {b,e}|\over \sqrt{|{a,b,d}| |{b,e}|}} = {1 \over \sqrt6} $
$W_{AD} = {|{a,b,d} \cap {c,d,e}|\over \sqrt{|{a,b,d}| |{c,d,e}|}} = {1 \over 3} $
第二步,给学习者A推荐与之最相似的学习者的学习内容。由上步骤可知,学习者D与A最详细,那么就可以考虑将学习者D学习过的知识点c或e推荐给学习者A。这里便是基于用户的协同过滤算法的核心,公式如下:
$p(u,i) = \sum_{v \in S(u,K) \cap N(i)} w_{uv}r_{vi}$
其中,p(u,i) 表示学习者u对知识点i的适应度,S(u,k) 表示和学习者u相似的K个学习者,N(i) 表示对知识点i有过学习行为的学习者集合,$w_{uv}$表示学习者u和学习者v之间的相似度,$r_{vi}$表示学习者v对知识点的适应度,为了简化运算,$r_{vi}$取值为1。
根据基于用户的协同过滤算法,可以分别求出学习者A对于知识点c与知识点e的适应度:
$p(A,c) = w_{AB} + w_{AD} = 1.075$
$p(A,e) = w_{AC} + w_{AD} = 1.075$
两者相等,因此智慧学习系统给学习者A推荐知识点c或者知识点c皆可。
接下来使用 python 实现基于用户的协同过滤算法,嵌入智慧学习系统进行测试。
首先,编程模拟数据集,这里模拟了10000个学习者对100个知识点的学习行为及其学习效果,总计300000条数据,生成模拟数据集代码如下:
#-*-coding:utf-8-*-
import random
i = 0
with open("student_score_knowledge", "w") as f:
k = 0
while k < 100:
j = 0
while j < 10000:
if random.randint(1, 10) > 7:
f.write(str(j) + "," + str(random.randint(1, 100)) + "," + str(k) + '\n')
j += 1
k += 1
代码生成的数据集的前10条数据如下图所示。
5,68,0
8,9,0
12,44,0
15,28,0
18,69,0
22,78,0
26,93,0
32,12,0
33,96,0
40,1,0第一列是学习者的id,取值0~9999;第二列是学习行为评价分,取值0~100分;第三列为知识点id,取值0~99。
之后编写基于用户的协同过滤算法代码,给9088号学习者推荐教育信息资源,python 语言实现如下:
# -*-coding:utf-8-*-
from math import sqrt
fp = open("student_score_knowledge", "r")
users = {}
for line in open("student_score_knowledge"):
lines = line.strip().split(",")
if lines[0] not in users:
users[lines[0]] = {}
users[lines[0]][lines[2]] = float(lines[1])
class recommender:
# data:数据集,这里指users
# k:表示得出最相近的k的近邻
# metric:表示使用计算相似度的方法
# n:表示推荐知识点的个数
def __init__(self, data, k=3, metric='pearson', n=10):
self.k = k
self.n = n
self.username2id = {}
self.userid2name = {}
self.productid2name = {}
self.metric = metric
if self.metric == 'pearson':
self.fn = self.pearson
if type(data).__name__ == 'dict':
self.data = data
def convertProductID2name(self, id):
if id in self.productid2name:
return self.productid2name[id]
else:
return id
# 定义的计算相似度的公式,用的是皮尔逊相关系数计算方法
def pearson(self, rating1, rating2):
sum_xy = 0
sum_x = 0
sum_y = 0
sum_x2 = 0
sum_y2 = 0
n = 0
for key in rating1:
if key in rating2:
n += 1
x = rating1[key]
y = rating2[key]
sum_xy += x * y
sum_x += x
sum_y += y
sum_x2 += pow(x, 2)
sum_y2 += pow(y, 2)
if n == 0:
return 0
# 皮尔逊相关系数计算公式
denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)
if denominator == 0:
return 0
else:
return (sum_xy - (sum_x * sum_y) / n) / denominator
def computeNearestNeighbor(self, username):
distances = []
for instance in self.data:
if instance != username:
distance = self.fn(self.data[username], self.data[instance])
distances.append((instance, distance))
distances.sort(key=lambda artistTuple: artistTuple[1], reverse=True)
return distances
# 推荐算法的主体函数
def recommend(self, user):
# 定义一个字典,用来存储推荐知识点和分数
recommendations = {}
# 计算出user与所有其他学习者的相似度,返回一个list
nearest = self.computeNearestNeighbor(user)
# print nearest
userRatings = self.data[user]
totalDistance = 0.0
# 得住最近的k个近邻的总距离
for i in range(self.k):
totalDistance += nearest[i][1]
if totalDistance == 0.0:
totalDistance = 1.0
# 将与user最相近的k个人中user没有学过的知识点推荐给user,并且这里又做了一个分数的计算排名
for i in range(self.k):
# 第i个人的与user的相似度,转换到[0,1]之间
weight = nearest[i][1] / totalDistance
# 第i个人的name
name = nearest[i][0]
# 第i个学习者学习的知识点和相应的分数
neighborRatings = self.data[name]
for artist in neighborRatings:
if not artist in userRatings:
if artist not in recommendations:
recommendations[artist] = (neighborRatings[artist] * weight)
else:
recommendations[artist] = (recommendations[artist] + neighborRatings[artist] * weight)
recommendations = list(recommendations.items())
recommendations = [(self.convertProductID2name(k), v) for (k, v) in recommendations]
# 做了一个排序
recommendations.sort(key=lambda artistTuple: artistTuple[1], reverse=True)
return recommendations[:self.n], nearest
def adjustrecommend(id):
knowledgeId_list = []
r = recommender(users)
k, nearuser = r.recommend("%s" % id)
for i in range(len(k)):
knowledgeId_list.append(k[i][0])
return knowledgeId_list, nearuser[:15]
if __name__ == '__main__':
knowledgeId_list, near_list = adjustrecommend("9088")
print ("knowledgeId_list:", knowledgeId_list)
print ("near_list:", near_list)
运行结果如下:
('knowledgeId_list:', ['97', '94', '59', '66', '20', '57', '14', '47', '89', '87', '64', '25'])
('near_list:', [('4718', 1.0000000000000002), ('4746', 1.0), ('7914', 1.0), ('3758', 1.0), ('2626', 1.0), ('4679', 0.9999999999999999), ('2758', 0.9845887954432616), ('1019', 0.975116672724719), ('3855', 0.9680997288628137), ('5414', 0.9641935241787112), ('4503', 0.9563196022040577), ('1884', 0.9526930844027075), ('5000', 0.9493272875239307), ('3586', 0.9458761763543502), ('4319', 0.9443018954078959)])因此可知,可以给9088号学习者推荐97号、94号、59号、66号、20号、57号、14号、47号、89号、87号、64号、25号知识点,同时与9088号学习者学习行为最契合的前15个学习者的编号为:4718、4746、7914、3758、2626、4679、2758、1019、3855、5414、4503、1884、5000、3586、4319。
综上,在智慧学习系统中运用基于用于的协同过滤算法,不仅可以得到应该给某位学习者推荐的知识点内容,也可以知道学习者之间的相似性。
5.3.2 基于物品的协同过滤算法
然而学习者行为数据每时每刻都在更新,要在短周期内维护这样一个大量的数据集会消耗巨大的成本,那么有什么更好的方式去为学习者推荐知识点呢?答案是有的,运用基于物品的协同过滤算法。相对于学习行为表,知识网络静态的成分更加多一些,因此维护一张知识网络表会比维护学习行为表的代价要低廉。
基于物品的协同过滤算法,即是通过不同学习对知识点的学习去评测知识点之间的相似性与关联性,简而言之就是给学习者推荐它之前学习过的知识点相似性及关联性较高的其他知识点。
现举一例,以说明基于物品的协同过滤算法的原理及其在智慧学习系统中的应用。同样的,我们举5.3.1中提及的例子,表格如下:
| 学习者 | 学习行为 |
|---|---|
| A | a,b,d |
| B | a,c |
| C | b,e |
| D | c,d,e |
第一步,构建知识点的同现矩阵:
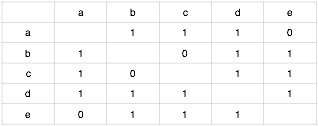
第二步,按照知识点间的余弦相似度公式$W_{ij}={|N(i) \cap N(j)| \over |N(i)|}$可对矩阵做归一化处理,其中分母是学习了知识点i的学习者数目,分子是同时学习了知识点i和知识点j的学习者数目。处理结果如下:
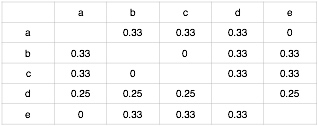
同时根据学习者学习行为建立学习者A对知识点的评分矩阵,这里没有学习到的知识点直接评为0分,评分矩阵如下:
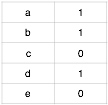
第三步,根据基于物品协同过滤算法的公式$p(u,j) = \sum_{j \in N(u) \cap S(j,K)} w_{ji}r_{ui}$来计算学习者u对知识点j的适应度,这里的 N(u) 是学习者学习过的知识点的集合,S(j,K)是和知识点j相似性关联性最高的知识点的集合,$w_{ji}$是知识点j和知识点i的相似度,$r_{ui}$是学习者是否对该知识点有过学习行为。推荐结果即为同现矩阵乘以评分矩阵,结果如下:
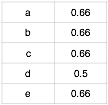
现对学习者A进行知识点推荐,去除学习者A学习过的知识点a、b、d,剩下的c、e推荐指数均为0.66,因此给学习者A推荐知识点c或者知识点e皆可。这里可见,基于物品的协同过滤算法与基于用户的协同过滤算法推荐的知识点差异不大。
接着,使用5.3.1中的300000条学习记录的数据集,为1308号学习者推荐教育信息资源。在智慧学习系统中使用 python 语言实现基于物品的协同过滤算法,代码如下:
# -*-coding:utf-8-*-
import math
class ItemBasedCF:
def __init__(self, train_file):
self.train_file = train_file
self.readData()
def readData(self):
# 读取文件,并生成用户-物品的评分表和测试集
self.train = dict() # 用户-物品的评分表
for line in open(self.train_file):
user, score, item = line.strip().split(",")
self.train.setdefault(user, {})
self.train[user][item] = int(float(score))
def ItemSimilarity(self):
# 建立物品-物品的共现矩阵
C = dict() # 物品-物品的共现矩阵
N = dict() # 物品被多少个不同用户购买
for user, items in self.train.items():
for i in items.keys():
N.setdefault(i, 0)
N[i] += 1
C.setdefault(i, {})
for j in items.keys():
if i == j: continue
C[i].setdefault(j, 0)
C[i][j] += 1
# 计算相似度矩阵
self.W = dict()
for i, related_items in C.items():
self.W.setdefault(i, {})
for j, cij in related_items.items():
self.W[i][j] = cij / (math.sqrt(N[i] * N[j]))
return self.W
# 给用户user推荐,前K个相关用户
def Recommend(self, user, K=3, N=10):
rank = dict()
action_item = self.train[user] # 用户user产生过行为的item和评分
for item, score in action_item.items():
for j, wj in sorted(self.W[item].items(), key=lambda x: x[1], reverse=True)[0:K]:
if j in action_item.keys():
continue
rank.setdefault(j, 0)
rank[j] += score * wj
return dict(sorted(rank.items(), key=lambda x: x[1], reverse=True)[0:N])
# 声明一个ItemBased推荐的对象
Item = ItemBasedCF("student_score_knowledge")
Item.ItemSimilarity()
recommedDic = Item.Recommend("1308")
for k, v in recommedDic.iteritems():
print k, "\t", v
输出结果如下:
20 44.0523484005
57 68.1684743338
30 34.8929285855
62 36.300574704
40 70.1473341065
75 46.1939495104
53 35.8462593001
80 43.5841206362
31 36.5522592084
79 72.8229228948第一列数据为应为1308号学习者推荐的知识点编号,第二列数据为推荐指数,指数越大,越值得推荐。至此,智慧学习系统便可以向1308号学习者推荐相关的教育信息资源了。
5.4 混沌蚁群算法
蚁群算法是一种基于群体智能的搜索复杂网络中的最短路径算法,它和 Dijkstra 有所不同,Dijkstra 算法只能够规划静态路径,而在学习生活中,系统所需要规划的路径往往是动态的,Dijkstra 算法并不能适应路径的动态变化。蚁群算法图例如下,F是蚁穴起点,N是目标食物源。开始一批的蚂蚁属混沌状态,随机行走,但蚂蚁在行走时在路径上留下信息素,单位时间内有固定数目的蚂蚁从蚁穴出发,它们会行走选择信息素最浓的路径。最短路径耗时最短,信息素越多,因此整个蚁群将会逐渐收敛到最短路径上。

在智慧学习系统中应用蚁群算法的流程图如下所示:
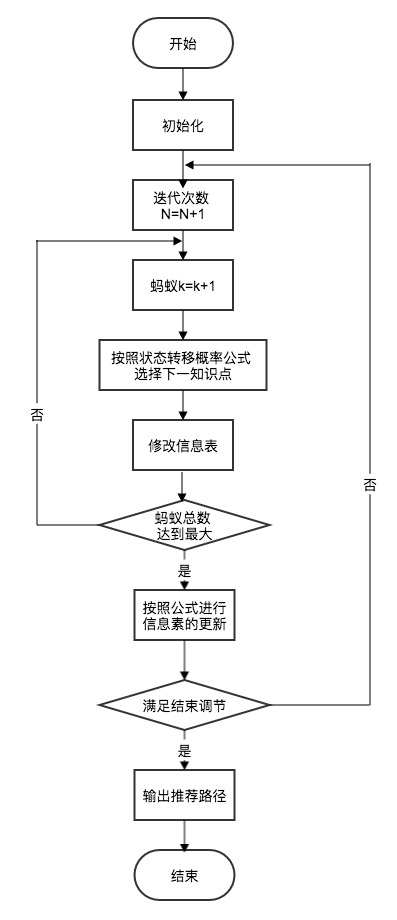
对于单个蚂蚁而言,它在复杂网络中是一个混沌的个体,而单个学习者在复杂的知识网络中也是一个混沌的个体,若是无人指导,只能盲目前进。但是对于一群蚂蚁而言,复杂网络的混沌性就被消除了,它们总可以在复杂网络中找到最优的路径。下表为学习路径推荐与蚂蚁觅食之间的关系[5]:
| 学习路径推荐 | 蚂蚁觅食 |
|---|---|
| 学习者 | 蚂蚁 |
| 学习目标 | 食物 |
| 评价信息 | 信息素 |
| 路径推荐 | 觅食最优路径 |
在文献[5]中,提供了基于蚁群算法的学习者路径推荐算法,其将 m 只蚂蚁随机放在 N 个知识点上,位于知识点i上的蚂蚁选择下一个知识点j的转移概率公式与信息素更新规则公式,此处不再赘述。
5.5 推荐算法评测与优化
5.5.1 Top-N 推荐性能评测
对学习者 u 推荐 N 个知识点记为$R(u)$,令学习者 u 在测试集上学习的知识点的集合为$T(u)$,然后便可以通过召回率与准确率来评测推荐算法的性能:
$Recall = {\sum_u | R(u) \cap T(u) | \over \sum_u | T(u)|}$
$Precision = {\sum_u | R(u) \cap T(u) | \over \sum_u | R(u)|}$
对于以上公式的解释,简而言之就是:召回率 = 提取出的正确信息条数 / 样本中的信息条数,正确率 = 提取出的正确信息条数 / 提取出的信息条数。接下来,根据公式检测一下用户协同过滤算法的性能。
首先设计并生成模拟数据,代码如下:
#-*-coding:utf-8-*-
import random
import numpy as np
import datetime
start = datetime.datetime.now()
studentNumber = 100
knowledgeNumber = 120
tiggerPrecision = 0.9
limitPrecision = 0.75
maxScore = 10000
key = np.full((1, knowledgeNumber/3), tiggerPrecision)
precision = np.random.random((studentNumber, knowledgeNumber))
for studentId in range(0, studentNumber):
if (precision[studentId][:knowledgeNumber/3] > key[0][:]).any():
max = np.amax(precision[studentId][:knowledgeNumber/3])
precision[studentId][:knowledgeNumber/3] = np.random.randint(int(limitPrecision)*10000, 10000, (1, knowledgeNumber/3)) / 10000.0
precision[studentId][random.randint(0, knowledgeNumber/3-1)] = max
if (precision[studentId][knowledgeNumber/3:knowledgeNumber/3*2] > key[0][:]).any():
max = np.amax(precision[studentId][knowledgeNumber/3:knowledgeNumber/3*2])
precision[studentId][knowledgeNumber/3:knowledgeNumber/3*2] = np.random.randint(int(limitPrecision)*10000, 10000, (1, knowledgeNumber/3)) / 10000.0
precision[studentId][random.randint(knowledgeNumber/3, knowledgeNumber/3*2-1)] = max
if (precision[studentId][knowledgeNumber/3*2:knowledgeNumber] > key[0][:]).any():
max = np.amax(precision[studentId][knowledgeNumber/3*2:knowledgeNumber])
precision[studentId][knowledgeNumber/3*2:knowledgeNumber] = np.random.randint(int(limitPrecision)*10000, 10000, (1, knowledgeNumber/3)) / 10000.0
precision[studentId][random.randint(knowledgeNumber/3*2, knowledgeNumber-1)] = max
print 'round1:' + str(studentId)
data = np.zeros((studentNumber, knowledgeNumber))
for studentId in range(0, studentNumber):
for knowledgeId in range(0, knowledgeNumber):
if random.random() > precision[studentId][knowledgeId]:
data[studentId][knowledgeId] = random.randint(1, maxScore)
print 'round2:' + str(studentId)
precision = np.round(precision, 5)
data = np.floor(data)
np.save("precision.npy", precision)
np.save("data.npy", data)
end = datetime.datetime.now()
print 'run time:' + str(end-start)
以上python代码模拟了100个学习者针对120个知识点的学习行为评分,这里的学习行为评分是一种综合式的系统评分,根据学习者针对某个知识点学习的各项指标生成评分,范围于1~10000之间,并将数据使用 numpy 存于 data.npy 文件中。需要注意的是,此处我将120个知识点根据id分成了3组,学习者总有一定的概率学习某个知识点,若他学习某个知识点的概率在90%以上,则他再学习该组其他知识点的概率也会相应的调整为75%以上的某个数值,以此给知识点间增加了某种关联,使这120个知识点构成3组知识网络。同时,这种学习概率在模拟数据中,可以等效取代为 Top-N 推荐中的准确率,因此,将学习者学习知识点的概率使用 numpy 存于 precision.npy 文件中。
接着编写 make_data.py 处理数据格式,代码如下:
#-*-coding:utf-8-*-
import numpy
data = numpy.load('data.npy')
knowledgeNumber = data.shape[1]
studentNumber = data.shape[0]
with open("student_score_knowledge", "w") as f:
for knowledgeId in range(0, knowledgeNumber):
for studentId in range(0, studentNumber):
if data[studentId][knowledgeId] != 0:
f.write(str(studentId) + "," + str(int(data[studentId][knowledgeId])) + "," + str(knowledgeId) + '\n')
最后运行 5.3.1 中编写好的协同过滤算法推荐程序 usercf.py,给15号学习推荐知识点,结果如下:
('knowledgeId_list:', ['63', '53', '60', '77', '118', '30', '69', '65', '106', '116', '20', '7'])
('near_list:', [('50', 0.495707633134417), ('22', 0.49405209142961004), ('23', 0.4236795382571208), ('14', 0.39008940674960735), ('58', 0.37840091215692845), ('54', 0.32396752155837233), ('83', 0.3178091063892354), ('68', 0.31539851554062515), ('89', 0.30208074596031165), ('53', 0.2672660961137338), ('5', 0.26310053523070887), ('84', 0.2349285437389371), ('24', 0.2291665096357303), ('6', 0.22327100302824932), ('26', 0.2220300365327438)])可见和15号学习者学习行为相似的有50号、22号、23号学习者等,其中与50号最为相似相似率为49.57%,推荐15号学习者的知识点为63号、53号、60号等,其中63号推荐概率最高,那么就根据15号学习者与推荐的63号知识点来计算 Top-N,编码 precision.py 如下:
# -*- coding: utf-8 -*-
import numpy as np
precisions = np.load('precision.npy')
# 15号学习者学习63号知识点的准确率(概率)
precision = precisions[15][63]
print(precision)
运行以上程序,控制台打印结果为:0.98456。因此,该系统在100%召回率下,对15号学习者的推荐精度达98.456%。为了系统测试的科学性,此处我们改造一下 usercf.py 的main函数代码,分别对100位学习者进行推荐:
if __name__ == '__main__':
# knowledgeId_list, near_list = adjustrecommend("15")
# print ("knowledgeId_list:", knowledgeId_list)
# print ("near_list:", near_list)
recommendKnowledgeId = []
for studentId in range(0, 100):
knowledgeId_list, near_list = adjustrecommend(str(studentId))
recommendKnowledgeId.append(knowledgeId_list[0])
np.save('recommend.npy', recommendKnowledgeId)
print(recommendKnowledgeId)
打印结果如下:
['74', '31', '88', '37', '76', '92', '80', '97', '27', '8', '23', '102', '27', '30', '61', '63', '35', '52', '48', '91', '39', '94', '24', '41', '78', '12', '72', '87', '75', '69', '80', '58', '99', '35', '52', '82', '33', '43', '78', '45', '72', '71', '82', '35', '17', '10', '35', '117', '59', '86', '101', '11', '104', '35', '28', '45', '95', '104', '40', '10', '10', '86', '94', '74', '31', '43', '53', '71', '39', '80', '78', '49', '76', '80', '78', '33', '73', '15', '15', '74', '35', '25', '62', '35', '77', '56', '108', '3', '10', '72', '83', '76', '35', '59', '64', '12', '35', '103', '65', '81']此处改写 precision.py 计算100次推荐的精度和算术平均数,得到系统在100%召回率下的平均推荐精度:
import numpy as np
precisions = np.load('precision.npy')
recommend = np.load('recommend.npy')
StudentNumber = 1000
total = 0
for studentId in range(0, StudentNumber):
knowledgeId = int(recommend[studentId])
precision = precisions[studentId][knowledgeId]
total = total + precision
print(total / StudentNumber)
输出结果为:0.67814,即系统在100%召回率情况下,推荐精度为67.814%。当然,这仅仅是只有100个学习者学习数据的情况之下的系统精度,若有1000个学习者,再次进行测试,最终结果为69.212%,提高了1.4个百分点。编码将 student_score_knowledge 文件中记录数随机减少25%,最终程序输出结果为:0.57039619,即在召回率75%的情况下,系统推荐精度为57.04%。
同理,调整召回率,绘制出以下图表:
| Recall | Precision |
|---|---|
| 100% | 69.21% |
| 90% | 64.17% |
| 80% | 62.29% |
| 70% | 60.37% |
| 60% | 57.98% |
| 50% | 56.72% |
| 40% | 56.24% |
| 30% | 53.83% |
| 20% | 53.30% |
| 10% | 52.49% |
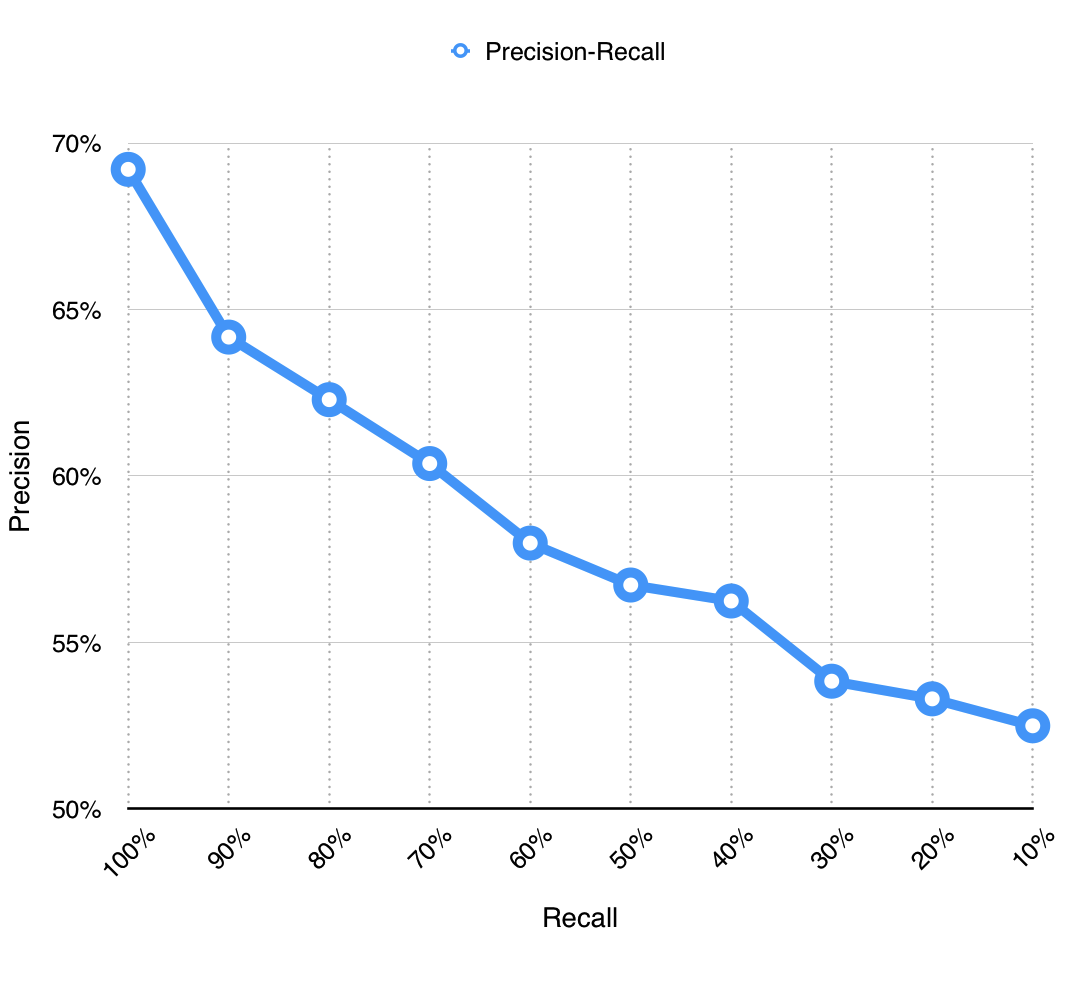
智慧学习系统具有海量的数据,所以在性能不能对全部数据进行分析处理,所以召回率会很低,而召回率越低,推荐的准确率也越低。但哪怕只有10%召回率,也有高于50%的准确性,已经足够满足学习者的需求。
至此,可将计算召回率与准确率的 python 代码嵌入到智慧学习系统之中,对算法的性能进行评定。
5.5.2 算法改进与优化探究
通过对用户协同过滤算法的性能测试,我们发现了一些可能存在的问题。推荐系统中无论是物品还是用户都会存在长尾现象[21],即学习越活跃的学习者会比较高概率学到冷门的知识,越热门、越广泛的知识点越会推荐给更多的学习者。所以,还可通过计算推荐覆盖率来进行对系统评估:$Coverage = {|R(u)|\over|I|}$,即推荐出去的知识点数目/全部知识点数目。覆盖率反映了推荐算法发掘长尾的能力,覆盖率越高,说明推荐算法越能够将长尾中的知识点推荐给学习者。覆盖率与算法中的K值和N值有关,K值和N值代表该学习者会向与他相似的K个学习者推荐N个知识点。在之前的算法实现中,默认设置了K值为3,N值为10。通过编程,计算此时系统覆盖率:
# -*- coding: utf-8 -*-
import numpy as np
recommend = np.load('recommend.npy')
knowledgeNumber = 120.0
print(len(np.unique(recommend)) / knowledgeNumber)
运行之后控制台打印结果为:0.991666666667,即覆盖率高达99.17%,这是由于学习者过多,而知识点过少导致的。此时,将学习者数目由1000调整回100,再次运行程序,得到覆盖率为:50%。
通过调整K值和N值,计算100%召回率下 Top-N 的系统性能指标,首先固定N值为10,调整K值:
| K值 | N值 | 准确率 | 覆盖率 |
|---|---|---|---|
| 1 | 10 | 68.78% | 53.33% |
| 2 | 10 | 65.06% | 51.67% |
| 3 | 10 | 68.78% | 50% |
| 4 | 10 | 64.59% | 50% |
| 5 | 10 | 67.88% | 48.33% |
| 6 | 10 | 65.99% | 52.50% |
| 7 | 10 | 63.74% | 47.50% |
| 8 | 10 | 64.95% | 48.33% |
| 9 | 10 | 67.50% | 49.17% |
| 10 | 10 | 66.74% | 47.50% |
可见在K值为1时,准确率和覆盖率都比较高。接着固定K值为1,调整N值:
| N值 | K值 | 准确率 | 覆盖率 |
|---|---|---|---|
| 1 | 1 | 68.78% | 53.33% |
| 2 | 1 | 68.78% | 53.33% |
| 3 | 1 | 68.78% | 53.33% |
| 4 | 1 | 68.78% | 53.33% |
| 5 | 1 | 68.78% | 53.33% |
| 6 | 1 | 68.78% | 53.33% |
| 7 | 1 | 68.78% | 53.33% |
| 8 | 1 | 68.78% | 53.33% |
| 9 | 1 | 68.78% | 53.33% |
| 10 | 1 | 68.78% | 53.33% |
据此可知,覆盖率和准确率和N值无关,因此可以将N值固定为1,减少运算量,从而优化算法性能。同时可根据实际情况调整K值,增加算法的准确率和覆盖率。
对于协同过滤算法,还需要对余弦相似度的公式进行一些个性化定制。如5.3.1与5.3.2的例子中,给学习者A推荐知识点,计算之后发现知识点c、e的推荐度完全一致。一方面是因为示例中数据量过少的缘故,另一方法是余弦相似度计算时分母的权重略大。如基于物品的协同过滤算法中,有些知识点属于通用知识点,很多学习者都会学习,这样通用知识点的推荐指数天然的就会比其他的知识点推荐指数要高。因此,对于5.3.2中物品相似度计算公式:$w_{ij} = {|N(i) \cap N(j)| \over |N(i)|}$,可将其优化为:$w_{ij} = {|N(i) \cap N(j)| \over \sqrt{|N(i)| |N(j)|}}$,该公式惩罚了知识点j的权重,因此减轻了通用知识点与很多知识点相似的可能性。
对于混沌蚁群算法,其和遗传算法相比,遗传算法在种群进化的初期有着快速的全局搜索能力,而在后期搜索速度较慢。蚁群算法则是前期信息匮乏速度慢,后期则快速收敛。所以可考虑将两种算法结合,通过遗传算法算子的选择、交叉、变异来改进蚁群算法的参数。
以上推荐算法实现匆匆,尚有许多的不足之处,但该在线学习资源智慧推送系统的框架与核心已经具备,待未来系统实现之后,可再根据具体使用场景进行优化。
6 总结
通过以上研究,得出了智慧学习系统的基本框架,分析了系统推送的基本流程,解析了系统数据层的存储设计与数据流的处理模型。之后,使用系统聚类算法对学习者进行聚类分析研究,并使用Gini系数对学习者进行特征选择,从而实现学习者建模。随后,谈论了知识网络的三种模型,并使用Apriori算法对知识节点进行关联分析。最后,分析并实现了系统核心的推送算法,包括Dijkstra单源最短路径算法、蚁群算法、协同过滤算法,测试过程中模拟了大量真实情景下的数据,并采用了Top-N测试对基于用户协同过滤算法进行准确率、召回率、覆盖率的检测,并进行参数调优。
至此,系统建模研究已经完成,基本架构与核心功能皆已实现,核心代码可直接嵌入未来的智慧学习系统中。但国内外尚未有一个完整的智慧学习系统,所以系统性能方面需要更多的研究,以便未来可以顺利实现智慧学习系统,并真正地投入使用。
参考文献
[1] 刁楠楠, 熊才平, 丁继红,等. 基于智慧信息推送的个性化学习服务实证研究——以“文献选读与论文写作”课程为例[J]. 中国远程教育, 2016(3):22-27. [2] 黄荣怀, 杨俊锋, 胡永斌. 从数字学习环境到智慧学习环境——学习环境的变革与趋势[J]. 开放教育研究, 2012, 18(1):75-84. [3] 黄荣怀. 智慧教育的三重境界:从环境、模式到体制[J]. 现代远程教育研究, 2014(6):3-11. [4] 贺斌. 智慧学习:内涵、演进与趋向——学习者的视角[J]. 电化教育研究, 2013(11):24-33. [5] 赵铮, 李振, 周东岱,等. 智慧学习空间中学习行为分析及推荐系统研究[J]. 现代教育技术, 2016, 26(1):100-106. [6] 冯翔, 吴永和, 祝智庭. 智慧学习体验设计[J]. 中国电化教育, 2013(12):14-19. [7] 赵秋锦, 杨现民, 王帆. 智慧教育环境的系统模型设计[J]. 现代教育技术, 2014, 24(10):12-18. [8] 郁晓华, 顾小清. 学习活动流:一个学习分析的行为模型[J]. 远程教育杂志, 2013(4):20-28. [9] Xin Dong, Lei Yu, Zhonghuo Wu, Yuxia Sun, Lingfeng Yuan, Fangxi Zhang. A Hybrid Collaborative Filtering Model with Deep Structure for Recommender Systems[R], AAAI, 2017 [10] 项亮. 推荐系统实践[M]. 北京:人民邮电出版社,2012 [11] Massa P, Avesani P. Trust-aware recommender systems[C], ACM Conference on Recommender Systems. ACM, 2007:17-24. [12] John S. Breese, David Heckerman, Carl Kadie. Empirical Analysis of Predictive Algorithms for Collaborative Filtering[C]. San Francisco: Morgan Kaufmann Publishers Inc, 1998 [13] Harry Huang. 使用LFM(Latent factor model)隐语义模型进行Top-N推荐[OL]. http://blog.csdn.net/harryhuang1990/article/details/9924377 [14] Taher H. Haveliwala. Topic-Sensitive PageRank[D]. Palo Alto: Stanford University, 2002 [15] Morgan Ames, Mor Naaman. Why we tag: motivations for annotation in mobile and online media[C]. New York: ACM, 2007 [16] Dae-joonHwang. What’s the Implication of “SMART” in Education and Learning?[EB/OL].[2013-03-10]. http://www.elearningasia.net/_program/pdf_pt/[Panelist%203-2]Dae-joon%20Hwang.pdf.[17] Oliver K,Hannafin M.Developing and refining mental models in open-ended learning environments:A case study[J]. Educational Technology Research and Development,2001,(4):5-32. [18] Perkins D N.Technology meets constructivism: Do they make a marriage[J]. Constructivism and the technology of instruction:A conversation,1992:45-55. [19] Jonassen D.Designing constructivist learning environments[J]. Instructional design theories and models:A new paradigm of instructional theory,1999,(2):215-239. [20] 陈琦,张建伟. 信息时代的整合性学习模型——信息技术整合于教学的生态观诠释[J]. 北京大学教育评论,2003,(3):90-96. [21] 杨开城. 建构主义学习环境的设计原则[J]. 中国电化教育,2000,(4):14-18. [22] 钟志贤. 论学习环境设计[J]. 电化教育研究,2005,(7):35-41. [23] 武法提. 论目标导向的网络学习环境设计[J]. 电化教育研究,2013,(7):40-46. [24] 彭文辉,杨宗凯,黄克斌. 网络学习行为分析及其模型研究[J]. 中国电化教育,2006,(10):31-35. [25] 数据分析联盟. 用户画像实例:创建可信的微博用户画像[OL]. http://mp.weixin.qq.com/mp/appmsg/show?__biz=MjM5NTczNjE5Mw==&appmsgid=10000224&itemidx=4&sign=77e84dea95e7d1277ba72c278c3980eb&3rd=MzA3MDU4NTYzMw==&scene=6#wechat_redirect [26] 王富平. 一号店用户画像系统实践[OL]. http://mp.weixin.qq.com/s?__biz=MzA4Mzc0NjkwNA==&mid=402350940&idx=2&sn=349553a14c163b20551a270b45dfa877&3rd=MzA3MDU4NTYzMw==&scene=6#rd [27] 邱盛昌. 电商大数据应用之用户画像[OL]. http://www.imooc.com/learn/460 [28] Wikipedia. Apache Hadoop[OL]. https://en.wikipedia.org/wiki/Apache_Hadoop [29] Wikipedia. MapReduce[OL]. https://en.wikipedia.org/wiki/MapReduce [30] Kit_Ren. Hadoop大数据平台架构与实践—基础篇[OL]. http://www.imooc.com/learn/391 [31] Craig Chambers, Ashish Raniwala, Frances Perry. FlumeJava: Easy, Efficient Data-Parallel Pipelines[J]. ACM,2010:363-375. [32] R Albert, AL Barabasi. Statistical mechanics of complex networks[J]. Reviews of Modern Physics,2002,74:47-97. [33] D Watts, S Strogatz. Collective Dynamics of Small-World Networks[J]. Nature,1998,393:440-442. [34] AL Barabási, R Albert. Emergence of scaling in random networks[J]. Science,1999,286 (5439):509-512. [35] 徐鹏,王以宁. 大数据视角分析学习变革——美国《通过教育数据挖掘和学习分析促进教与学》报告解读及启示[J]. 远程教育杂志,2013(6)
致谢
本毕业论文和作品设计是在导师梁斌老师的悉心指导下完成的,从课题的选择到完成,梁斌老师给予了我细心的指导和不懈的支持。在毕业设计遇到瓶颈之时,也是梁斌老师给予了我莫大的帮助。梁斌老师为人热心、治学严谨的精神足够我一生受用。再多的言语也不能表达对恩师的感激之情!
感谢广州大学实验中心和计算机学院,在我的编程开发的道路上,四年来给予了我莫大的帮助,无论是实验室场所和设备的提供还是指导老师的支持,都给了我极大的帮助和鼓励。
感谢家人和同学对我的支持,让我顺利地完成本科四年的学业。
声明
本文作者邓国雄,著于2017年4月28日,该文为教育技术学专业的本科毕业论文。
未经许可,不得以任何形式进行转载与引用。